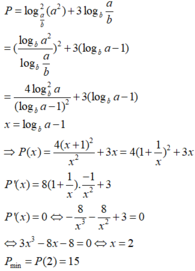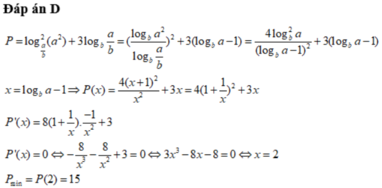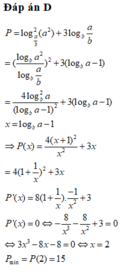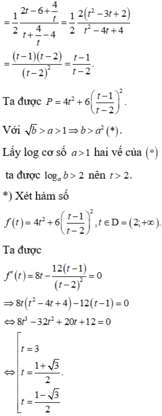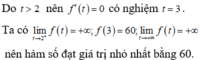Cho các số thực a, b thỏa mãn: a+b=1 Tìm giá trị nhỏ nhất của biểu thức: P= a³ + b³ + a³ + b³
HG
Những câu hỏi liên quan
câu1:
a) Cho các số thực không âm a, b, c thỏa mãn a + b + c =1. Tìm giá trị lớn nhất và giá trị nhỏ
nhất của biểu thức:
P=\(\frac{ab+bc+ca-abc}{a+2b+c}\)
b) Cho các số thực a, b, c thỏa mãn \(^{a^2+b^2+c^2=1}\)
Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức P =ab +bc + ca .
Cho các số thực a, b thỏa mãn
3
16
b
a
1
. Tìm giá trị nhỏ nhất của biểu thức
P
log
a
16
b
-
3
256
+
16
log
2
b
a
a
. A. 15...
Đọc tiếp
Cho các số thực a, b thỏa mãn 3 16 < b < a < 1 . Tìm giá trị nhỏ nhất của biểu thức P = log a 16 b - 3 256 + 16 log 2 b a a .
A. 15
B. 16
C. 17
D. 18
Cho a,b là các số thực thỏa mãn a≥1,b≥2. Tìm giá trị nhỏ nhất của biểu thức P=\(a^2\)+\(b^2\)+\(\dfrac{1}{a+b}\)+\(\dfrac{1}{b}\)
Lời giải:
Áp dụng BĐT Cô-si:
$a^2+1\geq 2a$
$b^2+4\geq 4b$
$\Rightarrow a^2+b^2\geq 2a+4b-5$
$\Rightarrow P\geq 2a+4b-5+\frac{1}{a+b}+\frac{1}{b}$
$=\frac{a+b}{9}+\frac{1}{a+b}+(\frac{b}{4}+\frac{1}{b})+\frac{17}{9}a+\frac{131}{36}b-5$
$\geq 2\sqrt{\frac{1}{9}}+2\sqrt{\frac{1}{4}}+\frac{17}{9}a+\frac{131}{36}b-5$
$=\frac{2}{3}+1+\frac{17}{9}a+\frac{131}{36}b-5$
$\geq \frac{2}{3}+1+\frac{17}{9}+\frac{131}{36}.2-5=\frac{35}{6}$
Vậy $P_{\min}=\frac{35}{6}$ khi $a=1; b=2$
Đúng 2
Bình luận (0)
Xét các số thực a, b thỏa mãn a b 1. Tìm giá trị nhỏ nhất của biểu thức
P
log
a
b
2
a
2
+
3
log
b
a
b
.
A. ...
Đọc tiếp
Xét các số thực a, b thỏa mãn a > b > 1. Tìm giá trị nhỏ nhất của biểu thức P = log a b 2 a 2 + 3 log b a b .
A. P min = 19.
B. P min = 13.
C. P min = 14.
D. P min = 15.
Cho các số thực a, b thỏa mãn
2
5
a
b
1
. Tìm giá trị nhỏ nhất của biểu thức
T
27
log
a
b
2
b
+
log
b
8
5
a
−
2...
Đọc tiếp
Cho các số thực a, b thỏa mãn 2 5 < a < b < 1 . Tìm giá trị nhỏ nhất của biểu thức T = 27 log a b 2 b + log b 8 5 a − 2 25 − 3.
A. 11
B. 8
C. 9
D. 6
Xét các số thực a, b thỏa mãn
a
b
1
. Tìm giá trị nhỏ nhất của biểu thức
P
log
a
b
2
a
2
+
3
log
b
a
b
A.
P...
Đọc tiếp
Xét các số thực a, b thỏa mãn a > b > 1 . Tìm giá trị nhỏ nhất của biểu thức P = log a b 2 a 2 + 3 log b a b
A. P m i n = 19
B. P m i n = 13
C. P m i n = 14
D. P m i n = 15
Xét các số thực a, b thỏa mãn a b 1. Tìm giá trị nhỏ nhất của biểu thức
P
log
a
b
2
(
a
2
)
+
3
log
b
a
b
A. ...
Đọc tiếp
Xét các số thực a, b thỏa mãn a> b > 1. Tìm giá trị nhỏ nhất của biểu thức P = log a b 2 ( a 2 ) + 3 log b a b
A. P m i n = 19
B. P m i n = 13
C. P m i n = 14
D. P m i n = 15
Tìm giá trị nhỏ nhất của biểu thức
P
log
a
b
2
2
+
6
log
b
a
b
a...
Đọc tiếp
Tìm giá trị nhỏ nhất của biểu thức P = log a b 2 2 + 6 log b a b a 2 với a, b là các số thực thỏa mãn b > a > 1 .
A. 30.
B. 40.
C. 60.
D. 50
Xét các số thực a; b thỏa mãn a b 1 . Tìm giá trị nhỏ nhất Pmin của biểu thức
P
log
2
a
b
a
2
+
3
log
b
a
b
A. 19 B. 13 C. 14 D. 15
Đọc tiếp
Xét các số thực a; b thỏa mãn a> b> 1 . Tìm giá trị nhỏ nhất Pmin của biểu thức P = log 2 a b a 2 + 3 log b a b
A. 19
B. 13
C. 14
D. 15
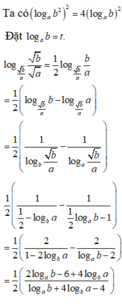
Ta có:
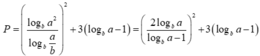
Đặt t= logba-1 > logbb -1=0 ,
khi đó:
P = 2 t + 2 t 2 + 3 t = f ( t ) f ' t = 2 . 2 t + 2 t . - 2 t 2 + 3 = 3 t 3 - 8 ( t + 1 ) t 3
F’ (t) =0 khi 3t3-8( t+1) =0 hay t= 2.
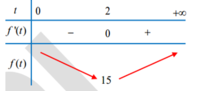
Suy ra Pmin =f(2) =15
Chọn D.
Đúng 0
Bình luận (0)