chứng tỏ 2 tia phân giác của 2 góc kề bù vuông góc với nhau
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
VV
Những câu hỏi liên quan
chứng tỏ rằng 2 tia phân giác của 2 góc kề bù thì vuông góc với nhau
Chứng tỏ rằng hai tia phân giác của 2 góc kề bù thì vuông góc với nhau.
Xét các tia x'ox và y'oy, có hai góc đối đỉnh là xoy và x'oy'
gọi ot và ot' là hai tia phân giác tương ứng
Thấy: góc xoy = góc x'oy'
=> góc yot = góc y'ot'
Ta có: góc xoy + góc xoy' = góc toy' + góc yot = 180o
<=> góc toy' + góc y'ot' = góc tot' = 180o
=> ot và ot' là hai tia đối nhau.
Đúng 0
Bình luận (0)
* Gọi góc xOz, góc zOy là 2 góc kề bù ; và tia Ou, Ov lần lượt là tia phân giác của góc xOz, zOy.
* Để chứng minh 2 tia phân giác của 2 góc kề bù vuông góc với nhau, ta sẽ chứng minh tia Ou vuông góc tia Ov.
* Vì tia Ou, Ov lần lượt là tia phân giác của góc xOz, zOy
nên:
{ góc uOz = 1/2 góc xOz
{ góc zOv = 1/2 góc zOy
Suy ra:
{ 2 góc uOz = góc xOz
{ 2 góc zOv = góc zOy
Ta lại có:
góc xOz + góc zOy = 180 độ (vì 2 góc xOz, góc zOy kề bù)
=> 2 góc uOz + 2 góc zOv = 180 độ
=> 2(góc uOz + góc zOv) = 180 độ
=> góc uOz + góc zOv = 90 độ
=> góc uOv = 90 độ (vì 2 góc uOz, góc zOv kề nhau)
=> Tia Ou vuông góc Tia Ov
Do đó, 2 tia phân giác của 2 góc kề bù thì vuông góc với nhau.
Đúng 0
Bình luận (0)
Góc kề bù là hình gồm 2 tia đối nhau
Và có tổng số đo là : 180 độ, có 1 cạnh chung
Vì tia phân giác là tia nằm giữa 2 tia còn lại và chia góc đó làm 2 phần bằng nhau
Tia phân giác của góc kề bù có số đo là:
180 : 2 = 90 độ
Vì góc có số đo là 90 độ là góc vuông
=> Tia phân giác của 2 góc kề bù vuông góc với nhau ( đpcm )
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Dùng kiến thức 2tia phân giác của 2 góc kề bù thì vuông góc với nhau.
1.Chứng tỏ : 2 tia phân giác của 2 góc đối đỉnh là 2 tia đối nhau.
Giả sử 2 dường thẳng xx' và yy' cắt nhau tại O
Kẻ Ot là tia fg góc xOy
và Ot' là tia fg góc x'Oy'. Ta phải chứng minh Ot và Ot' cùng nằm trên 1 đường thẳng hay tOt'=180o
tOt'=tOx+xOt' (tia Ox nằm giữa 2 tia Ot,Ot')
mà tOx=x'Ot' (cùng =1/2 hai góc đối đỉnh)
nên tOt'=x'Ot'+t'Ox=xOx'=180o (tia Ot' nằm giữa 2 tia Ox,Ox')
vậy Ot và Ot'là 2 tia đối nhau
Đúng 0
Bình luận (0)
Chứng tỏ hai tia phân giác của hai góc kề bù thì vuông góc với nhau
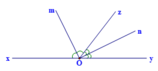
Xét Om và On thứ tự là tia phân giác của hai góc kề bù x O z ^ và z O y ^ . Ta có: x O z ^ + z O y ^ = 180 0 (hai góc kề bù) Mà Om là tia phân giác của x O z ^ => x O z ^ = 2 m O z ^ On là tia phân giác của z O y ^ ⇒ z O y ^ = 2 n O z ^ |
|
Do đó: 2 m O z ^ + 2 n O z ^ = 180 0
⇒ m O z ^ + n O z ^ = 90 0
⇒ m O n ^ = 90 0 ⇒ O m ⊥ O n
Vậy hai tia phân giác của hai góc kề bù thì vuông góc với nhau
Đúng 0
Bình luận (0)
Chứng tỏ rằng:Hai tia phân giác của hai góc kề bù thì vuông góc với nhau
Lật sách ra mà xem cho nha
Đúng 0
Bình luận (0)
* Gọi góc xOz, góc zOy là 2 góc kề bù ; và tia Ou, Ov lần lượt là tia phân giác của góc xOz, zOy.
* Để chứng minh 2 tia phân giác của 2 góc kề bù vuông góc với nhau, ta sẽ chứng minh tia Ou vuông góc tia Ov.
* Vì tia Ou, Ov lần lượt là tia phân giác của góc xOz, zOy
nên:
{ góc uOz = 1/2 góc xOz
{ góc zOv = 1/2 góc zOy
Suy ra:
{ 2 góc uOz = góc xOz
{ 2 góc zOv = góc zOy
Ta lại có:
góc xOz + góc zOy = 180 độ (vì 2 góc xOz, góc zOy kề bù)
=> 2 góc uOz + 2 góc zOv = 180 độ
=> 2(góc uOz + góc zOv) = 180 độ
=> góc uOz + góc zOv = 90 độ
=> góc uOv = 90 độ (vì 2 góc uOz, góc zOv kề nhau)
=> Tia Ou vuông góc Tia Ov
Do đó, 2 tia phân giác của 2 góc kề bù thì vuông góc với nhau.
Đúng 0
Bình luận (0)
Gỉa sử 2 góc kề bù là: xOy và yOz,phân giác Om và On ta có
xOy+yOz=xOm+yOm+yOn+zOn
xOm=yOm
yOn=zOn
Do đó xOm+zOn=yOm+yOn=180:2=90
Vậy hai tia phân giác của hai góc kề bù thì vuông góc với nhau
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
1.Cho 2 góc kề bù xOy và yOz. Ot là tia phân giác của xOy, vẽ Ot' vuông góc với Ot(Ot' và Ot thuộc cùng 1 nửa mặt phẳng bơ). Chứng tỏ Ot' là tia phân giác của yOz.
2.Chứng tỏ:2 tia phân giác của 2 góc đối đỉnh là 2 tia đối nhau.
1)Chứng minh rằng 2 tia phân giác của 2 góc kề bù vuông góc với nhau.
2)Cho AOC và COB kề bù, OM là phân giác của AOC, kẻ tia ON vuông góc với OM nằm trong góc BOC . Tia ON là tia phân góc của góc nào?Vì sao?
Gọi góc xOz, góc zOy là 2 góc kề bù ; và tia Ou, Ov lần lượt là tia phân giác của góc xOz, zOy.
* Để chứng minh 2 tia phân giác của 2 góc kề bù vuông góc với nhau, ta sẽ chứng minh tia Ou vuông góc tia Ov.
* Vì tia Ou, Ov lần lượt là tia phân giác của góc xOz, zOy
nên:
{ góc uOz = 1/2 góc xOz
{ góc zOv = 1/2 góc zOy
Suy ra:
{ 2 góc uOz = góc xOz
{ 2 góc zOv = góc zOy
Ta lại có:
góc xOz + góc zOy = 180 độ (vì 2 góc xOz, góc zOy kề bù)
=> 2 góc uOz + 2 góc zOv = 180 độ
=> 2(góc uOz + góc zOv) = 180 độ
=> góc uOz + góc zOv = 90 độ
=> góc uOv = 90 độ (vì 2 góc uOz, góc zOv kề nhau)
=> Tia Ou vuông góc Tia Ov
Do đó, 2 tia phân giác của 2 góc kề bù thì vuông góc với nhau.
Đúng 0
Bình luận (0)
chứng tỏ rằng tia phân giác của hai góc kề bù vuông góc với nhau
* Gọi góc xOz, góc zOy là 2 góc kề bù ; và tia Ou, Ov lần lượt là tia phân giác của góc xOz, zOy.
* Để chứng minh 2 tia phân giác của 2 góc kề bù vuông góc với nhau, ta sẽ chứng minh tia Ou vuông góc tia Ov.
* Vì tia Ou, Ov lần lượt là tia phân giác của góc xOz, zOy
nên:
{ góc uOz = 1/2 góc xOz
{ góc zOv = 1/2 góc zOy
Suy ra:
{ 2 góc uOz = góc xOz
{ 2 góc zOv = góc zOy
Ta lại có:
góc xOz + góc zOy = 180 độ (vì 2 góc xOz, góc zOy kề bù)
=> 2 góc uOz + 2 góc zOv = 180 độ
=> 2(góc uOz + góc zOv) = 180 độ
=> góc uOz + góc zOv = 90 độ
=> góc uOv = 90 độ (vì 2 góc uOz, góc zOv kề nhau)
=> Tia Ou vuông góc Tia Ov
Do đó, 2 tia phân giác của 2 góc kề bù thì vuông góc với nhau.
Đúng 0
Bình luận (0)
Bài 1: chứng tỏ rằng 2 tia phân giác của 2 góc kề bù thì vuông góc với nhau
Bài 2: cho góc tù AOB.Vẽ các tia OC,OD ở trong góc AOB sao cho OC vuông góc với OA;OD vuông góc OB
a, chứng tỏ góc AOB và COD bù nhau
b, vẽ tia Om, On lần lượt là các tia phân giác của các góc BOC; AOD.Chứng tỏ Om vuông góc với On
GIÚP MINK VỚI NHA! MỌI NGƯỜI, NHẤT LÀ BÀI 1 Í
MAI NỘP RÙI
Nếu bạn cần thì bạn lấy bài 1 trước nhá :
Gọi 2 góc kề bù lần lượt là A và B (cần có dấu mũ ở trên nhé)
Ta có: A + B = 180 (độ) <=> 1/2A + 1/2B = 1/2(A+B) = 90 (độ)
Vẽ hình ra là sẽ thấy ngay điều phải chứng minh !!
Đúng 0
Bình luận (0)


