rút gọn tổng: A=1+5^2+5^4+...+5^200
rút gọn A = 1+ 52+54+ .... + 5200
\(A=\left(1+5^2+5^4+...+5^{200}\right)\)
=>\(5^2.A=5^2.\left(1+5^2+5^4+...+5^{200}\right)\)
=>\(25A=5^2+5^4+5^8+...+5^{202}\)
=>\(25A-A=\left(5^2+5^4+5^6+...+5^{202}\right)-\left(1+5^2+5^4+...+5^{200}\right)\)
=>\(24A=5^{202}-1\Rightarrow A=\frac{5^{202}-1}{24}\)
1.Rút gọn tổng sau: 1 + 52 + 54 + 56 + 58 + ..... + 5200
2. So sánh: 222777 & 777222
1. Đặt A = 1 + 52 + 54 + ... + 5^200
Ta có: 52A = 52 + 54 + 56 + ... + 5^202
25A - A = (52 + 54 + ... + 5202) - (1 + 52 + ... + 5200)
24A = 5202 - 1 => A = (5202 - 1) : 24
2. Ta có : 777222 = (7772)111
222777= (2227)11111
Vì 7772 < 2227 => (2227)111 > (7772)111
=> 222777 > 777222
Rút gọn : 1+5^2+5^3+5^4+.....+5^200
Giúp mình giải bài này nhé các bạn.
1. Tìm số tự nhiên a có tính chất:
a + 30 và a - 11 đều cho ta kết quả là số chính phương.
2. Rút gọn tổng sau:
1 + 5 + 52 + 54 + 56 + 58 + .... + 5200
chi lam duoc bai 2 thôi
kết qua la:(5^201-5)/4
Rút gọn các biểu thức sau:
a ) ( 8 − 3 2 + 10 ) 2 − 5 b ) 0 , 2 ( − 10 ) 2 ⋅ 3 + 2 ( 3 − 5 ) 2 c ) 1 2 1 2 − 3 2 ⋅ 2 + 4 5 ⋅ 200 : 1 8 d ) 2 ( 2 − 3 ) 2 + 2 ⋅ ( − 3 ) 2 − 5 ( − 1 ) 4
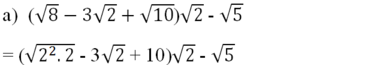
= (2√2 - 3√2 + 10)√2 - √5
= 2.(√2)2 - 3.(√2)2 + √10.√2 - √5
= 4 - 6 + √20 - √5 = -2 + 2√5 - √5
= -2 + √5
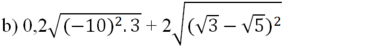
= 0,2.10.√3 + 2|√3 - √5|
s
= 2√3 + 2(√5 - √3)
= 2√3 + 2√5 - 2√3 = 2√5
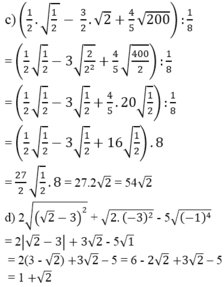
Rút gọn biểu thức sau
B = 1 + \(\frac{3}{2^3}+\frac{4}{2^4}+\frac{5}{2^5}+...+\frac{200}{2^{200}}\)
a) Rút gọn tổng A = 20 + 21 + 22 + 23 + .... 250
b) Rút gọn tổng B = 5 + 52 + 53 +..... +599+ 5100
c) Rút gọn tổng C = 3 - 32 + 33 - 34 .....+ 32007 - 32008 + 32009 - 32010
d) Rút gọn tổng S100 = 5 + 5 x 9 + 5 x 92 + 5 x 93+ ......5 x 999
\(A=2^0+2^1+2^2\)\(+2^3+...+\)\(2^{50}\)
\(2A=2+2^2+2^3+...+2^{51}\)
\(2A-A=A=2^{51}-2^0\)
\(B=5+5^2+5^3+...+5^{99}+5^{100}\)
\(5B=5^2+5^3+5^4+...+5^{100}+5^{101}\)
\(5B-B=4B=5^{101}-5\)
\(B=\frac{5^{101}-5}{4}\)
\(C=3-3^2+3^3-3^4+...+\)\(3^{2007}-3^{2008}+3^{2009}-3^{2010}\)
\(3C=3^2-3^3+3^4-3^5+...-3^{2008}+3^{2009}-3^{2010}+3^{2011}\)
\(3C+C=4C=3^{2011}+3\)
\(C=\frac{3^{2011}+3}{4}\)
\(S_{100}=5+5\times9+5\times9^2+5\times9^3+...+5\times9^{99}\)
\(S_{100}=5\times\left(1+9+9^2+9^3+...+9^{99}\right)\)
\(9S_{100}=5\times\left(9+9^2+9^3+...+9^{99}+9^{100}\right)\)
\(9S_{100}-S_{100}=8S_{100}=5\times\left(9^{100}-1\right)\)
\(S_{100}=\frac{5\times\left(9^{100}-1\right)}{8}\)
Thu gọn tổng sau
A= 1+52+54+56+....+5198+5200
Lời giải:
$A=1+5^2+5^4+5^6+...+5^{198}+5^{200}$
$5^2A=5^2+5^4+5^6+5^8+...+5^{200}+5^{202}$
$\Rightarrow 5^2A-A=5^{202}-1$
$\Rightarrow 24A=5^{202}-1$
$\Rightarrow A=\frac{5^{202}-1}{24}$
Thu gọn tổng sau:
A= 1+52+54+56+....+5198+5200