cho 2 số x,y thỏa mãn x+y=1
tìm giá trị nhỏ nhất của biểu thức M=5x^2+y^2
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
cho 2 số x , y thỏa mãn x+y=1
tìm giá trị nhỏ nhất của biểu thức M=5x^2+y^2
Ta có
x+y=1 => x=1-y
thay vào phương trình
\(\Rightarrow M=5.\left(1-y\right)^2+y^2\)
\(\Rightarrow M=5.\left(1-2y+y^2\right)+y^2\)
\(\Rightarrow M=5-10y+5y^2+y^2\)
\(\Rightarrow M=6y^2-10y+5\)
\(\Rightarrow M=6\left(y^2-\frac{5}{3}y+\frac{5}{6}\right)\)
\(\Rightarrow M=6\left(y^2-2.\frac{5}{6}y+\frac{25}{36}-\frac{25}{36}+\frac{5}{6}\right)\)
\(\Rightarrow M=6\left[\left(y-\frac{5}{6}\right)^2+\frac{5}{36}\right]\)
\(\Rightarrow M=6\left(y-\frac{5}{6}\right)^2+\frac{5}{6}\ge\frac{5}{6}\)
Vậy \(M_{min}=\frac{5}{6}\Leftrightarrow\hept{\begin{cases}x+y=1\\y-\frac{5}{6}=0\end{cases}\Leftrightarrow\hept{\begin{cases}x=1-y\\y=\frac{5}{6}\end{cases}}}\Leftrightarrow\hept{\begin{cases}x=1-\frac{5}{6}=\frac{1}{6}\\y=\frac{5}{6}\end{cases}}\)
T I C K chọn mình nha bạn cảm ơn chúc bạn học tốt
\(\)
Cho x, y là các số thực dương thỏa mãn 5 x + 2 y + 3 3 x y + x + 1 = 5 x y 5 + 3 − x − 2 y + x − 2 . Tìm giá trị nhỏ nhất của biểu thức T = x + y .
A. T min = 2 + 3 2 .
B. T min = 1 + 5 .
C. T min = 3 + 2 3 .
D. T min = 5 + 3 2 .
Đáp án C.
Ta có:
G T ⇔ 5 x + 2 y + x + 2 y − 3 − x − 2 y = 5 x y − 1 − 3 1 − x y + x y − 1.
Xét hàm số
f t = 5 t + t − 3 − t ⇒ f t = 5 t ln 5 + 1 + 3 − t ln 3 > 0 ∀ t ∈ ℝ
Do đó hàm số đồng biến trên ℝ suy ra f x + 2 y = f x y − 1 ⇔ x + 2 y = x y − 1
⇔ x = 2 y + 1 y − 1 ⇒ T = 2 y + 1 y − 1 + y . Do x > 0 ⇒ y > 1
Ta có: T = 2 + y + 3 y − 1 = 3 + y − 1 + 3 y − 1 ≥ 3 + 2 3 .
Cho x, y là các số thực dương thỏa mãn 5 x + 2 y + 3 3 x y + x + 1 = 5 x y 5 + 3 - x - 2 y + x - 2 . Tìm giá trị nhỏ nhất của biểu thức T = x + y.
![]()
![]()
![]()
![]()
Đáp án C.
Ta có: GT
<=> 5x+2y + x + 2y – 3–x–2y = 5xy–1 – 31–xy + xy – 1.
X é t h à m s ố f t = 5 t + t - 3 - t
⇒ f t = 5 t ln 5 + 1 + 3 - t ln 3 > 0 ∀ t ∈ ℝ
Do đó hàm số đồng biến trên ℝ suy ra
f(x+2y) = f(xy – 1) <=> x+ 2y = xy – 1
⇔ x = 2 y + 1 y - 1 ⇒ T = 2 y + 1 y - 1 + y .
Do x > 0 => y > 1.
Ta có:
T = 2 + y + 3 y - 1 = 3 + y - 1 + 3 y - 1 ≥ 3 + 2 3 .
Cho x, y là các số thực dương thỏa mãn điều kiện 5 x + 2 y + 3 3 x y + x + 1 = 5 x y 5 + 3 - x - 2 y + y ( x - 2 ) .Tính giá trị nhỏ nhất của biểu thức T = x + y
![]()
![]()
![]()
![]()
Đáp án B.
Từ giả thiết, suy ra
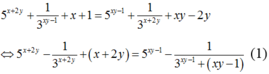
Xét hàm số f ( t ) = 5 t - 1 3 t + t trên ℝ .
Đạo hàm f ' ( t ) = 5 t . ln 5 - ln 3 3 t + 1 > 0 , ∀ t ∈ ℝ ⇒ hàm số f ( t ) luôn đồng biến trên ℝ .
Suy ra
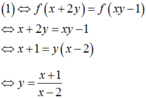
Do y > 0 nên x + 1 x - 2 > 0 ⇔ [ x > 2 x < - 1 . Mà x > 0 nên x > 2 .
Từ đó T = x + y = x + x + 1 x - 2 . Xét hàm số g ( x ) = x + x + 1 x - 2 trên 2 ; + ∞ .
Đạo hàm
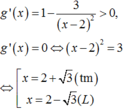
Lập bảng biến thiên của hàm số trên 2 ; + ∞ , ta thấy min g ( x ) = g ( 2 + 3 ) = 3 + 2 3 .
Vậy T m i n = 3 + 2 3 khi x = 2 + 3 và x = 1 + 3 .
Cho x, y là các số thực dương thỏa mãn điều kiện 5 x + 2 y + 3 3 x y + x + 1 = 5 x y 5 + 3 - x - 2 y + y ( x - 2 ) .
Tính giá trị nhỏ nhất của biểu thức T = x + y .
![]()
![]()
![]()
![]()
Cho x, y là các số thực dương thỏa mãn điều kiện 5 x + 2 y + 3 3 x y + x + 1 = 5 x y 5 + 3 − x − 2 y + y x − 2 . Tính giá trị nhỏ nhất của biểu thức T=x+y
A. T min = 2 + 3 2
B. T min = 3 + 2 3
C. T min = 3 2
D. T min = 5 + 3 2
Cho x, y là các số thực dương thỏa mãn điều kiện 5 x + 2 y + 3 3 x y + x + 1 = 5 x y 5 + 3 - x - 2 y + y x - 2 . Tính giá trị nhỏ nhất của biểu thức T = x + y
A. T m i n = 2 + 3 2
B. T m i n = 3 + 2 3
C. T m i n = 1 + 5
D. T m i n = 5 + 3 2
Đáp án B.
Từ giả thiết, suy ra 5 x + 2 y + 1 3 x y - 1 + x + 1 = 5 x y - 1 + 1 3 x + 2 y + x y - 2 y
⇔ 5 x + 2 y - 1 3 x + 2 y + x + 2 y = 5 x y - 1 - 1 3 x y - 1 + ( x y - 1 ) (1)
Xét hàm số f ( t ) = 5 t - 1 3 t + t trên ℝ .
Đạo hàm f ' ( t ) = 5 t . ln 5 + ln 3 3 t + 1 > 0 , ∀ t ∈ ℝ ⇒ hàm số f (t) luôn đồng biến trên ℝ .
Suy ra 1 ⇔ f ( x + 2 y ) = f ( x y - 1 ) ⇔ x + 2 y = x y - 1 ⇔ x + 1 = y ( x - 2 )
y = x + 1 x - 2
Do y > 0 nên x + 1 x - 2 > 0 ⇔ x > 2 x < - 1 . Mà x > 0 nên x > 2.
Từ đó T = x + y = x + x + 1 x - 2 . Xét hàm số g ( x ) = x + x + 1 x - 2 trên 2 ; + ∞ .
Đạo hàm g ' ( x ) = 1 - 3 x - 2 2 > 0 , g ' ( x ) = 0 ⇔ ( x - 2 ) 2 = 3
⇔ x = 2 + 3 ( t m ) x = 2 - 3 ( L ) . Lập bảng biến thiên của hàm số trên 2 ; + ∞ , ta thấy m i n g ( x ) = g ( 2 + 3 ) = 3 + 2 3 .
Vậy T m i n = 3 + 2 3 khi x = 2 + 3 và y = 1 + 3 .
Cho x,y là các số thực dương thỏa mãn điều kiện 5 x + 2 y + 3 3 x y + x + 1 = 5 x y 5 + 3 - x - 2 y + y x - 2
Tính giá trị nhỏ nhất của biểu thức T =x + y.
A. T m i n = 2 + 3 2
B. T m i n = 3 + 2 3
C. T m i n = 1 + 5
D. T m i n = 5 + 3 2
Từ giả thiết ta suy ra
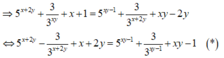
Xét hàm số f ( t ) = 5 t - 1 3 t + t với t ∈ ℝ , f ' ( t ) = 5 t . ln 5 + 3 - t . ln 3 + 1 > 0 ; ∀ t ∈ ℝ
Suy ra y= f( t) là hàm số đồng biến trên R mà từ ( * ) suy ra
f (x+ 2y) =f( xy-1) hay x+ 2y= xy-1
![]()
với x>0 suy ra y>1.
Khi đó
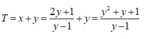
Xét hàm số
f ( y ) = y 2 + y + 1 y - 1 t r ê n 1 ; + ∞ f ' y = y 2 - 2 y - 2 y - 1 2 = 0 ⇔ y = ± 1 + 3 f 1 + 3 = 3 + 2 3 ; lim y → 1 f ( y ) = lim y → + ∞ f ( y ) = + ∞
Do đó, giá trị nhỏ nhất của hàm số là 3 + 2 3 .
Vậy kết quả là 3 + 2 3
Chọn B.
Cho các số tự nhiên x,y thỏa mãn x+y=101
Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức T=\(x^2-xy+y^2\)
Có xy ≤ 1/4 (x+y)^2
=> 3xy ≤ 3/4 (x+y)^2
=> T = x^2-xy+y^2 = (x+y)^2 - 3xy ≥ (x+y)^2 - 3/4 (x+y)^2 = 1/4 (x+y)^2
=10201/4
Dấu = xảy ra khi x=y=101/2
T = (x+y)^2 - 3xy <= (x+y)^2 = 101^2 = 10201
Dấu = xảy ra khi 1 số = 0, 1 số = 101