chứng minh rằng tổng hai cạnh bên hình thang lớn hơn hiệu hai đáy
NHANH NHA 2 tick
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
TN
Những câu hỏi liên quan
Chứng minh rằng tổng hai cạnh bên của hình thang lớn hơn hiệu của hai đáy.
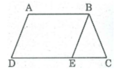
Giả sử hình thang ABCD có AB // CD
Từ B kẻ đường thẳng song song với AD cắt CD tại E.
Hình thang ABED có hai cạnh bên song song nên AB = ED và AD = BE
Ta có: CD – AB = CD – ED = EC (1)
Trong ∆ BEC ta có:
BE + BC > EC (bất đẳng thức tam giác)
Mà BE = AD
Suy ra: AD + BC > EC (2)
Từ (1) và (2) suy ra: AD + BC > CD – AB
Đúng 0
Bình luận (0)
chứng minh rằng tổng hai cạnh bên của hình thang lớn hơn hiệu hai đáy
Chứng minh rằng tổng hai cạnh bên của hình thang lớn hơn hiệu hai đáy ?
Vẽ hình thang ABCD nối B với D
Áp dụng bất đăng thức tam giác được:
BD + AB > AD (1)
BD + CD > BC (2)
Lấy (2) trừ (1) ta được:
BD + CD - BD - AB > BC - AD
\(\Leftrightarrow\) CD - AB > BC - AD
Đúng 0
Bình luận (0)
kẻ hình thang ABCD
kẻ 2 đường cao AH và BK nối B với H
xét tam giác ABH và tam giác KBH
có ^ABH = ^KBH ( 2gocs so le trong )
HB chung
=> tam giác ABH = tam giác KBH (cạnh huyền +góc nhọn )
=> AB =HK ( 2 cạnh tương ứng )
xét tam giác BKC có BC>KC ( trong tam giác vuông cạnh huyền là cạnh lớn nhất )(1)
xét tam giác AHD có AD>HD (trong tam giác vuông cạnh huyền là cạnh lớn nhất)(2)
từ (1) và (2) => BC+AD >KC+HD
ta lại có DH+DK +HK =DC
mà AB=HK (C/m )
=> DH+DK+AB =dc
ta có DC-AB = DH+DK+AB-AB= DH+DK
mà DH+DK<BC+AD(c/m)
=>DC -AB< BC+AD
vậy tổng hai cạnh bên của hình thang lớn hơn hiệu hai đáy
Đúng 0
Bình luận (0)
Chứng minh rằng tổng hai cạnh bên của hình thang lớn hơn hiệu hai đáy.
Chứng minh rằng tổng hai cạnh bên của hình thang lớn hơn hiệu hai đáy. Ai giúp mk vs. Mk đang cần gấp. Tks trc nha.
Vẽ hình thang ABCD nối B với D ( AB//CD)
Áp dụng BĐT tam giác ta có:
BD+AB>AD
BD+CD>BC
Trừ vế với vế ta được:
BD+CD-BD-AB>BC-AD
=> CD-AB>BC-AD (đđpcm)
Đúng 0
Bình luận (0)
Bn ơi, câu hỏi của mk là cm tổng hai cạnh bên > hiệu hai đáy mà bn. câu tl của bn là hiệu 2 cạnh đáy > hiệu 2 cạnh bên mà
Đúng 0
Bình luận (0)
Kẻ đường chéo BD
Áp dụng BĐT vào, ta có:
=> AB + DB > AD
DC + DB > BC
Trừ 2 vế với nhau:
AB + DB - DC - DB > AD - BC
=> AB - DC > AD - BC
=> AB - DC < AD + BC (đpcm)
Đúng 0
Bình luận (0)
chứng minh rằng tổng hai cạh bên của hình thang lớn hơn hiệu hai cạnh đáy
Chứng minh rằng tổng hai cạnh bên của hình thang lớn hơn hiệu của hai đáy.
Giả sử hình thang ABCD có AB // CD
Từ B kẻ đường thẳng song song với AD cắt CD tại E.
Hình thang ABED có hai cạnh bên song song nên AB = ED và AD = BE
Ta có: CD – AB = CD – ED = EC (1)
Trong ΔBEC ta có:
BE + BC > EC (bất đẳng thức tam giác)
Mà BE = AD
Suy ra: AD + BC > EC (2)
Từ (1) và (2) suy ra: AD + BC > CD – AB
Đúng 0
Bình luận (0)
Chứng minh rằng nếu hình thang có hai cạnh đáy không bằng nhau thì:
a/Tổng các cạnh bên lớn hơn hiệu hai cạnh đáy
b/Hiệu của đáy lớn và đáy nhỏ lớn hơn hiệu hai cạnh bên
c/Tổng hai đường chéo lớn hơn tổng hai đáy
Giúp minh nhanh đi mình đang cần gấp!
a, Trong hình thang ABCD (AB // CD), kẻ BE // AD
Ta có: BE = AD, AB = DE (hình thang có 2 cạnh bên song song)
Xét t/g BEC có: BE + BC > EC (BĐT tam giác)
=> AD + BC > CD - DE hay AD + BC > CD - AB (đpcm)
b, Xét t/g BEC có: EC < |BC - BE|
=> CD - AB < |BC - AD| (đpcm)
c,Kẻ BF // AC
=> AB = CF ; AC = BF (hình thang có 2 cạnh bên song song)
Xét t/g BDF có: BD + BF > DF (BĐT tam giác)
=> BD + AC > DF
=> BD + AC > DC + CF
=> BD + AC > DC + AB (đpcm)
Đúng 0
Bình luận (0)
Chứng minh rằng:
Nếu hình thang có 2 cạnh đáy không bằng nhau thì
a) Tổng các cạnh bên lớn hơn hiệu của hai đáy
b) Hiệu của đáy lớn và đáy nhỏ lớn hơn hiệu 2 cạnh bên
c) Tổng 2 đường chéo lớn hơn tổng 2 đáy





