1. Cho góc AOB tù. Vẽ các tia OC; OD ở trong góc AOB sao cho OC vuông góc với OA; OB vuông góc với OD
a. Chứng tỏ : Góc AOB và COD bù nhau
b. Vẽ OM, ON lần lượt là các tia phân giác của BOC:AOD
Chứng tỏ : OM vuông góc với ON
ớ miền trong của góc tù AOB vẽ các tia OC, OD sao cho OC vuông góc với OA, OD vuông góc với OB . Chứng tỏ rằng AOB +COD=180
Cho góc tù AOB, vẽ BOC và AOD là 2 góc kề bù với AOB. CMR : BOC và AOD là 2 góc đối đỉnh. Cho góc tù AOB. Trong góc AOB vẽ các tia OC và OD sao cho OC vuông góc vs OA, OD vuông góc vs OB.
Gọi Ox và Oy theo thứ tự là tia phân giác của AOD và BOC. ( Ko cần vẽ hình mn nhé!!)
Cho góc bẹt AOB. Vẽ tia OM sao cho MOA bằng MOB . vẽ tia OC nằm giữa hai tia OA, OM. Kể tên các góc vuông nhọn, tù ?
GÓC VUÔNG:
AOM, BOM
GÓC NHỌN:
AOC, COM
GÓC TÙ:
COB
Cho góc tù AOB. Vẽ các ti, OD, OC trong góc AOB sao cho OC vuông góc với OA, OD vuông góc với OB
a)Chứng minh rằng : góc AOB và COD bù nhau
b) Vẽ Om, On lần lượt là các tia phân giác của các góc BOC, AOD. CMR:Om vuông góc với On
a) Ta có : \(\hept{\begin{cases}\widehat{AOB}=90^o+\widehat{AOC}\\\widehat{COD}=90^o-\widehat{BOC}\end{cases}\Rightarrow\widehat{AOB}+\widehat{COD}=90^o+\widehat{AOC}+90^o-\widehat{BOC}=180^o\Rightarrowđpcm}\)
b) Ta có : \(\widehat{BOC}=\widehat{AOD}\) (cùng phụ nhau với \(\widehat{COD}\))
\(\Rightarrow\frac{\widehat{BOC}}{2}=\frac{\widehat{AOD}}{2}\Rightarrow\widehat{COM}=\widehat{AON}\) (phân giác On và On)
Lại có : \(\widehat{CON}+\widehat{AON}=90^o\Rightarrow\widehat{CON}+\widehat{COM}=90^o\) hay \(\widehat{mOn}=90^o\)
\(\Rightarrow Om\perp On\left(đpcm\right)\)
Cho góc tù AOB, A O B ^ = m ° . Vẽ vào trong góc này các tia OC, OD sao cho O C ⊥ O A ; O D ⊥ O B .
a) Chứng tỏ rằng A O D ^ = B O C ^ .
b) Tìm giá trị của m để A O D ^ = D O C ^ = C O B ^
a) Ta có O C ⊥ O A nên A O C ^ = 90 ° ; O D ⊥ O B nên B O D ^ = 90 ° .
Tia OD nằm trong góc AOB nên A O D ^ + B O D ^ = A O B ^ .
⇒ A O D ^ = A O B ^ − B O D ^ = m ° − 90 ° (1)
Tia OC nằm trong góc AOB nên A O C ^ + B O C ^ = A O B ^
⇒ B O C ^ = A O B ^ − A O C ^ = m ° − 90 ° (2)
Từ (1) và (2), suy ra: A O D ^ = B O C ^ = m ° − 90 °
b) Tia OC nằm giữa hai tia OB và OD. Suy ra B O C ^ + D O C ^ = B O D ^ = 90 ° .
Nếu B O C ^ = D O C ^ thì D O C ^ = 90 ° : 2 = 45 ° .
Do đó A O D ^ = D O C ^ = C O D ^ ⇔ A O B ^ = 3. D O C ^ = 3.45 ° = 135 ° ⇔ m = 135 .
Chứng tỏ hai đường thẳng vuông góc
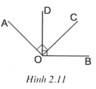
cho góc tù AOB. Vẽ các tia OC, OD ở trong góc AOB sao cho OC vuông góc với OA, OD vuông góc với OB
a, chứng minh rằng góc AOB và góc COD bù nhau
b, vẽ OM, ON lần lượt là các tia phân giác của góc BOC, góc AOC
c, chứng minh rằng OM vuông góc với góc ON
cho góc tù AOB. Vẽ các tia OC, OD ở trong góc AOB sao cho OC vuông góc với OA, OD vuông góc với OB
a, chứng minh rằng góc AOB và góc COD bù nhau
b, vẽ OM, ON lần lượt là các tia phân giác của góc BOC, góc AOC
c, chứng minh rằng OM vuông góc với góc ON
Trong góc tù AOB lần lượt vẽ các tia OC ; OD cho OC vuông góc OA và OD vuông góc OB
a, So sánh góc BOC và góc AOD
b, Vẽ tia OM là tia phân giác của góc AOB. Xét xem tia OM có phải là tia phân giác của góc COD không? Vì sao
Trong góc tù AOB lần lượt vẽ các tia OC ; OD cho OC vuông góc OA và OD vuông góc OB
a, So sánh góc BOC và góc AOD
b, Vẽ tia OM là tia phân giác của góc AOB. Xét xem tia OM có phải là tia phân giác của góc COD không? Vì sao