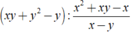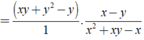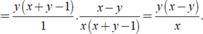Tìm các cặp số nguyên tố x, y:
x2+45=y2
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
SK
Những câu hỏi liên quan
Tìm các số nguyên tố x, y sao cho x2 + 45 = y2
Tham khảo:https://olm.vn/hoi-dap/detail/81346038854.html
Đúng 1
Bình luận (1)
Tìm các cặp số nguyên tố x, y sao cho: x^2-45=y^2
cho x,ý là các số nguyên tố thỏa mãn x2 +45 = y2 tính tổng x+y .
Thực hiện các phép tính sau? x y + y 2 - y : x 2 + x y - x x - y
Cho là các số nguyên tố x2 +45 =y2
thỏa mãn . Tổng .
Tìm các số nguyên tố x,y . Biết:
x2 + 117 = y2
Ta có :
Với x chẵn => x = 2 => 22 + 117 = y2
=> 121 = y2 => 112 = y2 => y = 11 (thoả mãn)
Với x lẻ => x2 cũng lẻ => x2 + 117 chẵn và x > 2
=> y2 chẵn => y = 2
Mà x < y => ko thoả mãn
Vậy x = 2 ; y = 11
Đúng 0
Bình luận (0)
Tìm tất cả các cặp số nguyên x, y thỏa mãn:
8|x - 2017| = 25 - y2
\(8\left|x-2017\right|=25-y^{2\text{}}\)
\(\Leftrightarrow8\left|x-2017\right|+y^2=25=25+0=24+1=21+4=16+9\)
Mà \(8\left|x-2017\right|\) chẵn nên ta có các trường hợp sau:
TH1: \(\left\{{}\begin{matrix}8\left|x-2017\right|=0\\y^2=25\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2017\\y=\pm5\end{matrix}\right.\)
TH2: \(\left\{{}\begin{matrix}8\left|x-2017\right|=24\\y^2=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}x=2020\\x=2014\end{matrix}\right.\\y=\pm5\end{matrix}\right.\)
TH3: \(\left\{{}\begin{matrix}8\left|x-2017\right|=16\\y^2=9\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}x=2019\\x=2015\end{matrix}\right.\\y=\pm3\end{matrix}\right.\)
Đúng 1
Bình luận (0)
tìm các cặp số nguyên x, y thỏa mãn: y2(x2-x+1)+xy = 3x-1
Bài 3*: Tìm các cặp số nguyên (x;y) thỏa mãn xy2 + 2x – y2 =