Xác định các hệ số a, b,c để:
(x2+cx+2)(ax+b)=x3-x2+2
TB
Những câu hỏi liên quan
Xác định các số a, b, c sao cho
1
(
x
2
+
1
)
(
x
-
1
)
a
x
+
b
x
2
+
1
+
c
x
-...
Đọc tiếp
Xác định các số a, b, c sao cho 1 ( x 2 + 1 ) ( x - 1 ) = a x + b x 2 + 1 + c x - 1
Ta có:
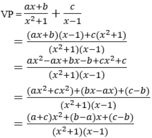
Đồng nhất phân thức trên với phân thức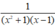 
ta được
Đúng 0
Bình luận (0)
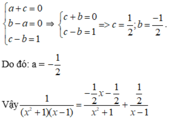
Xác định a, b, c, d để đồ thị của các hàm số:
y = x 2 + ax + b
và y = cx + d
cùng đi qua hai điểm M(1; 1) và B(3; 3).
a và b thỏa mãn hệ phương trình :
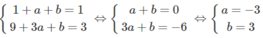
c và d thỏa mãn hệ phương trình:
Đúng 0
Bình luận (0)
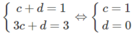
Tìm hệ số a,b,c biết
a, −3x2(2ax2−bx+c)=6x5+9x4−3c2∀x−3x2(2ax2−bx+c)=6x5+9x4−3c2∀x
b,(x2+cx+2)(a+b)=x3+x2−2∀x(x2+cx+2)(a+b)=x3+x2−2∀x
c,(ax2+bx+c)+(x+3)=x2+2x−3x∀x(ax2+bx+c)+(x+3)=x2+2x−3x∀x
Help me!!
bạn ghi lại đề đi mình chả hiểu cái mô tê gì cả
Đúng 0
Bình luận (0)
xác định a,b để đa thức f(x) =x3 +ax+b chia hết cho x2 +x-6
Phân tích đa thức x2+ x-6 = (x-2)(x+3)
Gọi thương của phép chia f(x) cho đa thức trên là Q(x)
Ta có f(2)= 8+ 2a+b=0
Suy ra 2a+b=-8
lại có f(-3)= -27+ 3a+b=0
Suy ra 3a+b=27
đến đây ta dùng máy tính giải hệ ta được a=35;b=-78
Đúng 0
Bình luận (0)
cho đa thức f(x)=ax^2+bx+c xác định hệ số a,b,c biết đa thức có 2 nghiệm x1=1: x2=2
`Answer:`
`f(x)=ax^2+bx+c`
Do đa thức `f(x)` có hai nghiệm là `x_1=1;x_2=2`
`=>(x-1)(x-2)=0`
`<=>x^2-2x-x+2=0`
`<=>x^2-3x+2=0`
Mà `f(x)=ax^2+bx+c`
Đồng nhất hệ số ta được \(\hept{\begin{cases}a=1\\b=-3\\c=2\end{cases}}\)
cho x1, x2 là 2 nghiệm dương của phương trình ax^2+bx+c=0
chứng minh phương trình cx^2+ax+b=0 cũng có 2 nghiệm dương x3,x4 và x1+x2+x3+x4>4 ?
a) ax^2 + bx + c = 0
Để phương trình thỏa mãn điều kiện có 2 nghiệm dương phân biệt.
∆ > 0
=> b^2 - 4ac > 0
x1 + x2 = -b/a > 0
=> b và a trái dấu
x1.x2 = c/a > 0
=> c và a cùng dấu
Từ đó ta xét phương trình cx^2 + bx^2 + a = 0
∆ = b^2 - 4ac >0
x3 + x4 = -b/c, vì a và c cùng dấu mà b và a trái dấu nên b và c trái dấu , vì vậy -b/c >0
x3.x4 = a/c, vì a và c cùng dấu nên a/c > 0
=> phương trình cx^2 + cx + a có 2 nghiệm dương phân biệt x3 và x4
Vậy nếu phương trình ax^2 + bx + c = 0 có 2 nghiệm dương phân biệt thì phương trình cx^2 + bx + a = 0 cũng có 2 nghiệm dương phân biệt.
b) Ta có, vì x1, x2, x3, x4 không âm, dùng cô si.
x1 + x2 ≥ 2√( x1.x2 )
x3 + x4 ≥ 2√( x3x4 )
=> x1 + x2 + x3 + x4 ≥ 2[ √( x1.x2 ) + √( x3x4 ) ] (#)
Tiếp tục côsi cho 2 số không âm ta có
√( x1.x2 ) + √( x3x4 ) ≥ 2√[√( x1.x2 )( x3.x4 ) ] (##)
Theo a ta có
x1.x2 = c/a
x3.x4 = a/c
=> ( x1.x2 )( x3.x4 ) = 1
=> 2√[√( x1.x2 )( x3.x4 ) ] = 2
Từ (#) và (##) ta có
x1 + x2 + x3 + x4 ≥ 4
Đúng 0
Bình luận (0)
Đưa các phương trình sau về dạng a
x
2
+ bx + c 0 và xác định các hệ số a, b, c: x +
m
2
x
2
+ m
x
2
+ mx + m + 2
Đọc tiếp
Đưa các phương trình sau về dạng a x 2 + bx + c = 0 và xác định các hệ số a, b, c: x + m 2 x 2 + m = x 2 + mx + m + 2
Cho P(x)=x4+x3-x2+ax+6
Q(x)=x2+x-2
Xác định a b để P(x)=Q(x)
Đề: Xác định các hệ số a,b,c biết:
b)(ax+b).(x2-x-1)=ax3+cx2-1