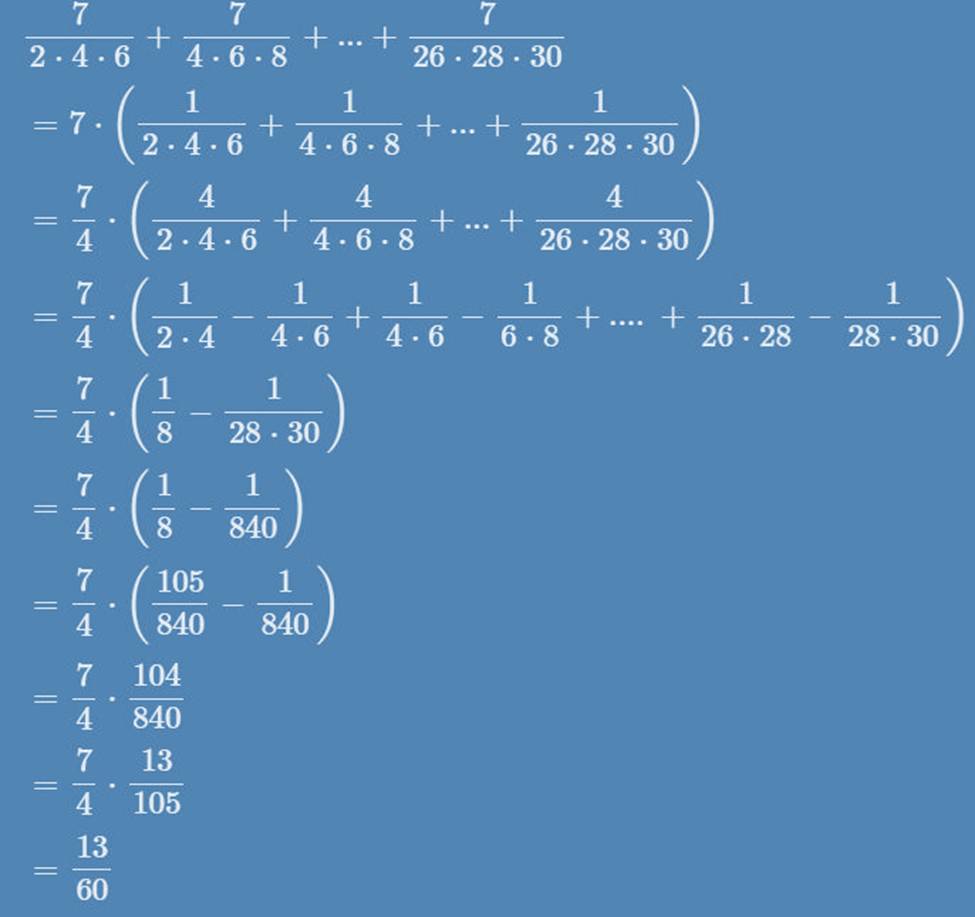So sánh
1/2.4.6+1/4.6.8+1/6.8.10+...+1/26.28.30 với 2
HT
Những câu hỏi liên quan
1/2.4.6 +1/4.6.8+1/6.8.10+1/8.10.12+1/10.12 .14+..1/96.98.100
\(\dfrac{7}{2.4.6}+\dfrac{7}{4.6.8}+...+\dfrac{7}{26.28.30}\)
Cho mình mỗi đáp án cũng được.
Tính nhanh: 5/2.4.6+5/4.6.8+5/6.8.10+...+5/20.22.24
\(A=\frac{2}{2.4.6}+\frac{2}{4.6.8}+\frac{2}{6.8.10}+\frac{2}{8.10.12}\)
\(A=\frac{2}{2.4.6}+\frac{2}{4.6.8}+\frac{2}{6.8.10}+\frac{2}{8.10.12}\)
\(A=\frac{2}{48}+\frac{2}{192}+\frac{2}{480}+\frac{2}{960}\)
\(A=\frac{1}{24}+\frac{1}{96}+\frac{1}{240}+\frac{1}{480}\)
\(A=\frac{20}{480}+\frac{5}{480}+\frac{2}{480}+\frac{1}{480}\)
\(A=\frac{7}{120}\)
Đúng 0
Bình luận (0)
A = \(\dfrac{2}{2.4.6}\) + \(\dfrac{2}{4.6.8}\) + \(\dfrac{2}{6.8.10}\) + \(\dfrac{2}{8.10.12}\)
A = \(\dfrac{2}{2}\).(\(\dfrac{2}{2.4.6}\) + \(\dfrac{2}{4.6.8}\) + \(\dfrac{2}{6.8.10}\) + \(\dfrac{2}{8.10.12}\))
A = \(\dfrac{1}{2}\).(\(\dfrac{2.2}{2.4.6}\) + \(\dfrac{2.2}{4.6.8}\) + \(\dfrac{2.2}{6.8.10}+\dfrac{2.2}{8.10.12}\))
A = \(\dfrac{1}{2}\).( \(\dfrac{4}{2.4.6}+\dfrac{4}{4.6.8}+\dfrac{4}{6.8.10}+\dfrac{4}{8.10.12}\))
A = \(\dfrac{1}{2}\).(\(\dfrac{1}{2.4}\) - \(\dfrac{1}{4.6}\) +\(\dfrac{1}{4.6}\) - \(\dfrac{1}{6.8}\) + \(\dfrac{1}{6.8}\) - \(\dfrac{1}{8.10}\) + \(\dfrac{1}{8.10}\) - \(\dfrac{1}{10.12}\))
A = \(\dfrac{1}{2}\).(\(\dfrac{1}{2.4}\) - \(\dfrac{1}{10.12}\))
A = \(\dfrac{1}{2}\).(\(\dfrac{1}{8}-\dfrac{1}{120}\))
A = \(\dfrac{1}{2}\).\(\dfrac{7}{60}\)
A = \(\dfrac{7}{120}\)
Đúng 0
Bình luận (0)
\(\frac{5}{2.4.6}+\frac{5}{4.6.8}+\frac{5}{6.8.10}\)
=5/48+5/192+5/480
=>9/24
tích đúng nha bạn
Đúng 0
Bình luận (0)
Cho A =4/2.4.6 +4/4.6.8+4/6.8.10+.......+4/46.48.50 tìm số nghịch đảo của A
Ta nhận thấy
\(\dfrac{1}{n\cdot\left(n+2\right)}-\dfrac{1}{\left(n+2\right)\cdot\left(n+4\right)}\\ =\dfrac{n+4}{n\cdot\left(n+2\right)\cdot\left(n+4\right)}-\dfrac{n}{n\cdot\left(n+2\right)\cdot\left(n+4\right)}\\ =\dfrac{n+4-n}{n\cdot\left(n+2\right)\cdot\left(n+4\right)}\\ =\dfrac{4}{n\cdot\left(n+2\right)\cdot\left(n+4\right)}\)
\(A=\dfrac{4}{2\cdot4\cdot6}+\dfrac{4}{4\cdot6\cdot8}+\dfrac{4}{6\cdot8\cdot10}+...+\dfrac{4}{46\cdot48\cdot50}\\ =\dfrac{1}{2\cdot4}-\dfrac{1}{4\cdot6}+\dfrac{1}{4\cdot6}-\dfrac{1}{6\cdot8}+\dfrac{1}{6\cdot8}-\dfrac{1}{8\cdot10}+...+\dfrac{1}{46\cdot48}-\dfrac{1}{48\cdot50}\\ =\dfrac{1}{2\cdot4}-\dfrac{1}{48\cdot50}\\ =\dfrac{1}{8}-\dfrac{1}{2400}\\ =\dfrac{300}{2400}-\dfrac{1}{2400}\\ =\dfrac{299}{2400}\)
Số nghịch đảo của \(A\) là \(\dfrac{2400}{299}\)
Đúng 0
Bình luận (0)
A=1.2.3-2.3.4+3.4.5-4.5.6+5.6.7/2.4.6-4.6.8+6.8.10-810.12+10.12.14
Trả lời nhanh cho mình ạ
A = \(\frac{2.4.6+4.6.8+6.8.10+8.10.12+...+198.200.202}{1.3.5+3.5.7+5.7.9+7.9.11+...+97.99.101}\) =?
Đề bài: Tính
2.4.6+4.6.8+6.8.10+...+98.100.102
XIN TRÌNH BÀY RÕ RÀNG! CẢM ƠN CÁC BẠN RẤT NHIỀU!