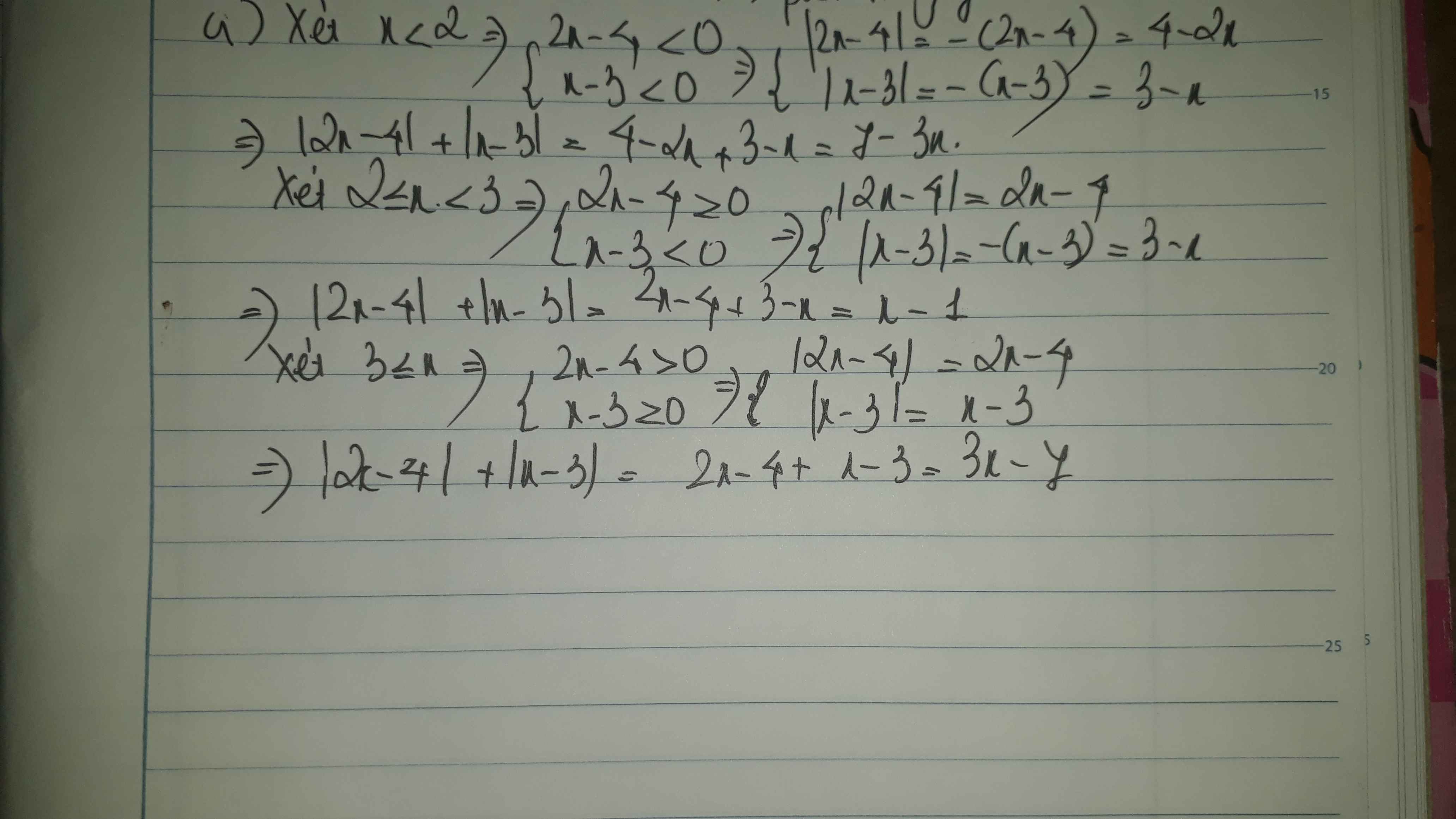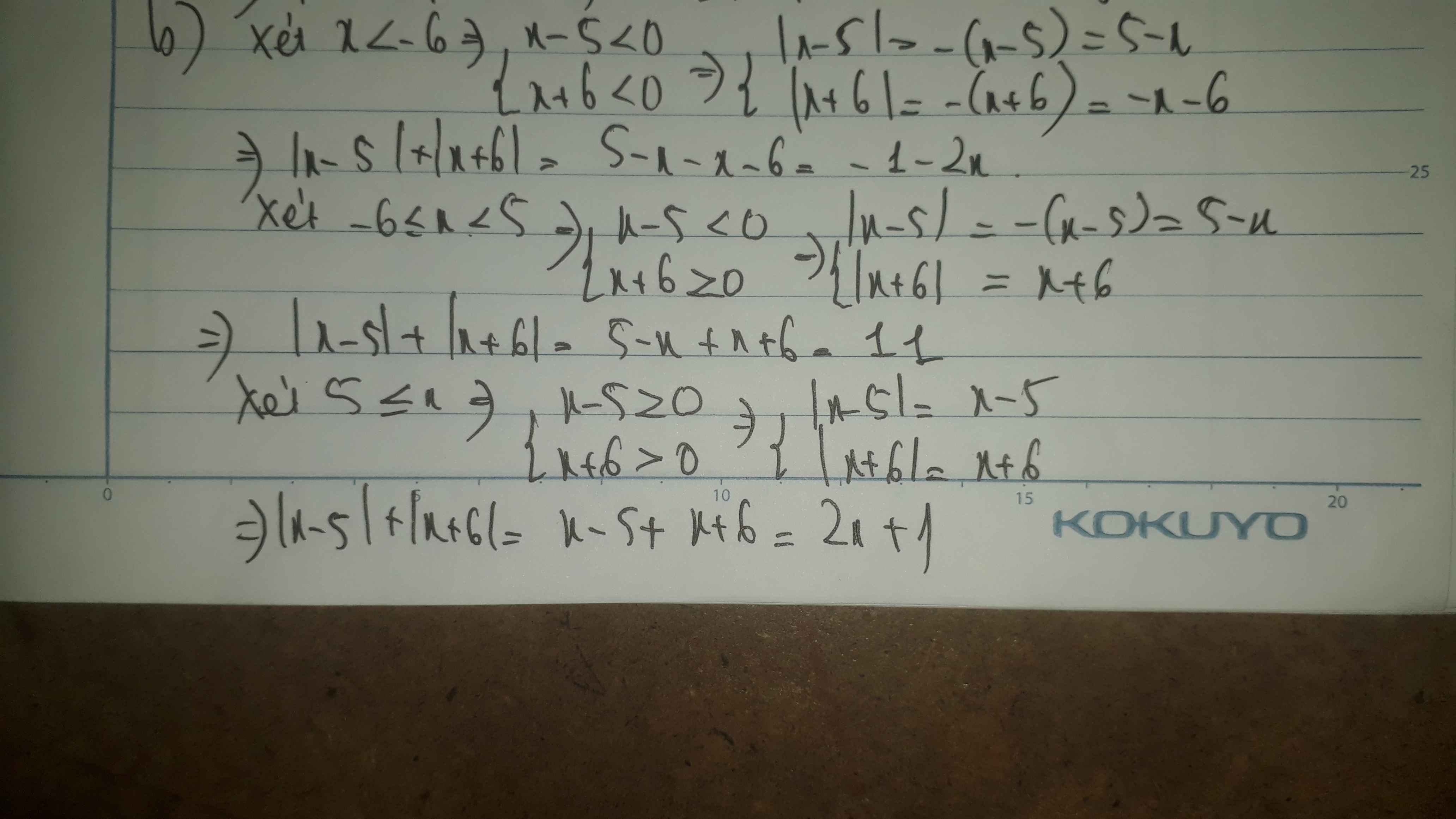Bỏ dấu giá trị tuyệt đối và rút gọn: A=|x-4| - 2x+12 khi x>5
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
NT
Những câu hỏi liên quan
Bỏ dấu giá trị tuyệt đối và rút gọn biểu thức: C = |x - 4| - 2x + 12 khi x > 5
- Khi x > 5 ta có x - 4 > 1 (trừ hai vế cho 4) hay x - 4 > 0 nên |x - 4| = x - 4
Vậy C = x - 4 - 2x + 12 = -x + 8
Đúng 0
Bình luận (0)
bỏ dấu giá trị tuyệt đối và rút gọn biểu thức:M=4+2x+l7-xl khi x>9
Khi x > 9 thì 7 - x < 0 do đó |7-x| = x - 7
Khi đó M=4+2x+l7-xl = 4 + 2x + x- 7 = 3x -3
Vậy M = 3x - 3
#Toán lớp 8
Đúng 0
Bình luận (0)
Bỏ dấu giá trị tuyệt đối và rút gọn các biểu thức sau: A = | 4x | - 2x + 12 với x < 0.
Ta có: x < 0 ⇒ | 4x | = - 4x
Khi đó ta có: A = | 4x | - 2x + 12 = - 4x - 2x + 12 = 12 - 6x
Vậy A = 12 - 6x.
Đúng 0
Bình luận (0)
Bỏ dấu giá trị tuyệt đối và rút gọn các biểu thức sau: A = | 4x | - 2x + 12 với x < 0.
Ta có: x < 0 ⇒ | 4x | = - 4x
Khi đó ta có: A = | 4x | - 2x + 12 = - 4x - 2x + 12 = 12 - 6x
Vậy A = 12 - 6x.
Đúng 0
Bình luận (0)
Bỏ dấu giá trị tuyệt đối và rút gọn biểu thức: B = |-4x| - 2x + 12 trong hai trường hợp: x ≤ 0 và x > 0;
- Khi x ≤ 0 ta có -4x ≥ 0 (nhân hai vế với số âm) nên |-4x| = -4x
Vậy B = -4x - 2x + 12 = -6x + 12
- Khi x > 0 ta có -4x < 0 nên |-4x| = -(-4x) = 4x
Vậy B = 4x - 2x + 12 = 2x + 12
Đúng 0
Bình luận (0)
Bỏ dấu giá trị tuyệt đối và rút gọn biểu thức sau: B = 3x - 1 + | - 2x | khi x < 0.
Khi x < 0 ta có - 2x > 0 nên | - 2x | = - 2x
Do đó B = 3x - 1 + | - 2x | = 3x - 1 - 2x = x - 1.
Đúng 0
Bình luận (0)
bỏ dấu giá trị tuyệt đối rồi rút gọn các biểu thức sau:a,|2x-4|+|x-3|;b, |x-5|+|x+6|
a. \(\left|2x-4\right|+\left|x-3\right|\)
Với \(x< 2\), biểu thức trở thành
\(-\left(2x-4\right)-\left(x-3\right)\)
\(=-2x+4-x+3\)
\(=-3x+7\)
Với \(2\le x< 3\), biểu thức trở thành
\(\left(2x-4\right)-\left(x-3\right)\)
\(=2x-4-x+3\)
\(=x-1\)
Với \(x\ge3\), biểu thức trở thành
\(\left(2x-4\right)+\left(x-3\right)\)
\(=2x-4+x-3\)
\(=3x-7\)
b. \(\left|x-5\right|+\left|x+6\right|\)
Với \(x< -6\), biểu thức trở thành
\(-\left(x-5\right)-\left(x+6\right)\)
\(=-x+5-x-6\)
\(=-2x-1\)
Với \(-6\le x< 5\), biểu thức trở thành
\(-\left(x-5\right)+\left(x+6\right)\)
\(=-x+5+x+6\)
\(=11\)
Với \(x\ge5\), biểu thức trở thành
\(\left(x-5\right)+\left(x+6\right)\)
\(=x-5+x+6\)
\(=2x+1\)
Đúng 0
Bình luận (0)
Bỏ dấu giá trị tuyệt đối và rút gọn các biểu thức:
a) A = 3x + 2 + |5x| trong hai trường hợp: x ≥ 0 và x < 0;
b) B = |4x| -2x + 12 trong hai trường hợp: x ≤ 0 và x > 0;
c) C = |x - 4| - 2x + 12 khi x > 5;
d) D = 3x + 2 + |x + 5|
Hướng dẫn giải:
a) A = 3x + 2 + |5x|
=> A = 3x + 2 + 5x khi x ≥ 0
A = 3x + 2 - 5x khi x < 0
Vậy A = 8x + 2 khi x ≥ 0
A = -2x + 2 khi x < 0
b) B = 4x - 2x + 12 khi x ≥ 0
B = -4x -2x + 12 khi x < 0
Vậy B = 2x + 12 khi x ≥ 0
B = -6x khi x < 0
c) Với x > 5 => x - 4 > 1 hay x - 4 dương nên
C = x - 4 - 2x + 12 = -x + 8
Vậy với x > 5 thì C = -x + 8
d) D= 3x + 2 + x+ 5 khi x + 5 ≥ 0
D = 3x + 2 - (x + 5) khi x + 5 < 0
Vậy D = 4x + 7 khi x ≥ -5
D = 2x - 3 khi x < -5
Đúng 0
Bình luận (0)
Hướng dẫn giải:
a) A = 3x + 2 + |5x|
=> A = 3x + 2 + 5x khi x ≥ 0
A = 3x + 2 - 5x khi x < 0
Vậy A = 8x + 2 khi x ≥ 0
A = -2x + 2 khi x < 0
b) B = 4x - 2x + 12 khi x ≥ 0
B = -4x -2x + 12 khi x < 0
Vậy B = 2x + 12 khi x ≥ 0
B = -6x khi x < 0
c) Với x > 5 => x - 4 > 1 hay x - 4 dương nên
C = x - 4 - 2x + 12 = -x + 8
Vậy với x > 5 thì C = -x + 8
d) D= 3x + 2 + x+ 5 khi x + 5 ≥ 0
D = 3x + 2 - (x + 5) khi x + 5 < 0
Vậy D = 4x + 7 khi x ≥ -5
D = 2x - 3 khi x < -5
Đúng 0
Bình luận (0)
Bỏ dấu giá trị tuyệt đối và rút gọn các biểu thức:
a) A = 3x + 2 + |5x| trong hai trường hợp: x ≥ 0 và x < 0;
b) B = |4x| -2x + 12 trong hai trường hợp: x ≤ 0 và x > 0;
c) C = |x - 4| - 2x + 12 khi x > 5;
d) D = 3x + 2 + |x + 5|
a) Ta có : A = 3x + 2 + |5x|
+ x ≥ 0 thì A = 3x + 2 + 5x
=> A = 8x + 2
+ x < 0 thì A = 3x + 2 - 5x
=> A = 2 - 2x
Đúng 0
Bình luận (0)
Ta có : A=3x+2 + |5x|
\(x\ge0\) thì A = 3x+2+5x
=>A=8x+2
x<0 thì A=3x+2-5x
=>A=2-2x
Đúng 0
Bình luận (0)
a)Trường hợp 1 : x\(\ge0\)
\(\Rightarrow A=3x+2+\left|5x\right|\)
\(\Rightarrow A=3x+2+5x\)
\(\Rightarrow A=8x+2\)
Trường hợp 2 : x<0
\(\Rightarrow A=3x+2+-5x\)
\(\Rightarrow A=-2x+2\)
b,c,d tương tự
Đúng 0
Bình luận (0)
Xem thêm câu trả lời