tìm X,Y,M trong phép tính sau
3XY xM=16YY
H24
Những câu hỏi liên quan
1. Tìm y biết: y × 60006 = 1a8bc9d7 × 6
2. Tìm x, y, m biết 3xy × m = 16yy
tim x,y trong các phép tinh sau:
3xy * m = 16yy
ai nhanh mk k cho
Viết kết quả của phép tính dưới dạng một lũy thừa:a)
9
2
:
3
2
b)
125
:
5
2
c)
x
m
+
n
:
x
n
(
x
≠
0
;
m
,
n
∈
N
)
d) ...
Đọc tiếp
Viết kết quả của phép tính dưới dạng một lũy thừa:
a) 9 2 : 3 2
b) 125 : 5 2
c) x m + n : x n ( x ≠ 0 ; m , n ∈ N )
d) y 2 m : y m ( y ≠ 0 ; m ∈ N )
Cho phép lai sau đây ở ruồi giấm: P:
A
b
a
B
X
M
X
m
×
A
B
a
b
X
M
Y
. Ở F1 có kiểu hình mang ba tính trạng lặn chiếm 1,25%. Kết l...
Đọc tiếp
Cho phép lai sau đây ở ruồi giấm: P: A b a B X M X m × A B a b X M Y . Ở F1 có kiểu hình mang ba tính trạng lặn chiếm 1,25%. Kết luận nào sau đây đúng?
A. Số cá thể đực mang 1 trong 3 tính trạng trội ở F1 chiếm 30%
B. Số cá thể cái mang cả ba cặp gen dị hợp ở F1 chiếm 2,5%.
C. Số cá thể cái mang kiểu gen đồng hợp về cả 3 cặp gen trên chiếm 21%.
D. Tần số hoán vị gen ở giới cái là 40%.
Đáp án B
- Áp dụng công thức A-B- = aabb + 0,5 ; A-bb=aaB- = 0,25 – aabb ( phép lai 2 cơ thể dị hợp 2 cặp gen)
Cách giải:
Kiểu hình mang 3 tính trạng lặn mà ruồi giấm đực không có hoán vị gen nên cho giao tử ab = 0,5 → giao tử cái ab = 0,1 → f= 0,2
aabb = 0,05 → A-B- = aabb + 0,5 = 0,55 ; A-bb=aaB- = 0,25 – aabb=0,2
Xét các phương án
A. Số cá thể đực mang 1 trong 3 tính trạng trội ở F1: 2×0,2×0,25XmY + 0,05×0,25XMY = 11,25% → A sai
B Số cá thể cái mang cả ba cặp gen dị hợp ở F1 : 2×0,5×0,1×0,25 =2,5% → B đúng
Đúng 0
Bình luận (0)
Cho hàm số
y
x
m
-
x
. Tìm m để hàm số đồng biến trên
1
;
+
∞
Đọc tiếp
Cho hàm số y = x m - x . Tìm m để hàm số đồng biến trên 1 ; + ∞
Tìm các chữ số x y trong phép tính sau x,y = y,x . 3 + 1,3
\(\overline{x,y}\) = \(y,x\) \(\times\) 3 + 1,3
10 \(\times\) \(\overline{x,y}\) = 10 \(\times\) ( \(\overline{y,x}\) \(\times\) 3 + 1,3)
\(\overline{xy}\) = \(\overline{yx}\) \(\times\) 3 + 13 => nếu \(x\) là chữ số lẻ thì y phải chẵn và ngược lại
\(\overline{yx}\) = ( \(\overline{xy}\) - 13) : 3
\(\overline{xy}\) ≤ 99 ⇒ \(\overline{yx}\) ≤ (99-13) : 3 = 28,66 ⇒ y =1; 2
Mặt khác ( \(\overline{xy}\) - 13 ) \(⋮\) 3 => \(x\) + \(y\) - 1 - 3 ⋮ 3 (1)
Thay \(y\) = 1 vào (1) ta có : \(x\) + 1 - 1 - 3 ⋮ 3
⇒ \(x\) ⋮ 3 ⇒ \(x\) = 3; 6; 9
vì y = 1 => \(x\) = 6 ( theo tính chẵn lẻ ở trên).
ta có : 6,1 = 1,6 \(\times\) 3 + 1,3 ( Đúng)
Thay y = 2 vào (1) ta có : \(x\) + 2 - 1 - 3 ⋮ 3 ⇒ \(x\) = 2; 5; 8
Vì y = 2 => \(x\) = 5 ( theo tính chẵn lẻ ở trên)
Ta có : 5,2 < 2,5 \(\times\) 3 + 1,3
=> y = 2; \(x=5\) loại
Vậy chữ số \(x\); \(y\) thỏa mãn đề bài là \(x\) = 6; y = 1
Đúng 0
Bình luận (0)
Cho đồ thị (C):
y
x
+
1
x
và đường thẳng (d): y-(x+1) . Biết (d) tiếp xúc (C) tại điểm M, tìm
x
M
.
Đọc tiếp
Cho đồ thị (C): y = x + 1 x và đường thẳng (d): y=-(x+1) . Biết (d) tiếp xúc (C) tại điểm M, tìm x M .
Cho hàm số
y
x
+
1
x
-
1
có đồ thị là (C). Gọi
M
(
x
M
;
y
M
)
là một điểm bất kỳ...
Đọc tiếp
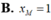
Cho hàm số y = x + 1 x - 1 có đồ thị là (C). Gọi M ( x M ; y M ) là một điểm bất kỳ trên (C). Khi tổng khoảng cách từ M đến hai trục tọa độ là nhỏ nhất, tính tổng x M + y M .
A. 
B. 
C. 
.
D. 
Viết kết quả của phép tính dưới dạng một lũy thừa:a,
9
2
:
3
2
b,
125
:
5
2
c,
x
m
+
n
:...
Đọc tiếp
Viết kết quả của phép tính dưới dạng một lũy thừa:
a, 9 2 : 3 2
b, 125 : 5 2
c, x m + n : x n x ≠ 0 ; m , n ∈ N
d, y 2 m : y m y ≠ 0 ; m ∈ N
a, 9 2 : 3 2 = 3 2 2 : 3 2 = 3 4 : 3 2 = 3 2
b, 125 : 5 2 = 5 3 : 5 2 = 5
c, x m
d, y m
Đúng 0
Bình luận (0)