Cho tam giác ABC có \(\widehat{A}\)= 60o; \(\widehat{B}\)= 80o và có phân giác AD
a) So sánh các cạnh của tam giác ADC
b) So sánh các cạnh của tam giác ADB
GJ
Những câu hỏi liên quan
Cho tam giác ABC, góc \(\widehat{B} \) = 60o, BC = 8cm, AB + AC = 12cm. Tính AB
Dựng \(AH\) vuông góc \(BC\). Đặt \(AB=x\Rightarrow AH=x.\sin60^0=\dfrac{x\sqrt{3}}{2};BH=x\cos60^0=\dfrac{x}{2}\)
\(\Rightarrow HC=BC-BH=8-\dfrac{x}{2};AC=12-x\)
Tam giác \(AHC\) vuông tại \(H\Rightarrow AC^2=AH^2+HC^2\Rightarrow\left(12-x\right)^2=\dfrac{3x^2}{4}+\left(8-\dfrac{x}{2}\right)^2\)
Giải phương trình trên ta được \(x=5\).
Vậy \(AB=5cm\).
Đúng 3
Bình luận (0)
Cho hình lăng trụ tam giác ABC. ABC có BB a, góc giữa đường thẳn BB và mặt phẳng (ABC) bằng
60
o
, tam giác ABC vuông tại C và
B
A
C
^
60
o
. Hình chiếu vuông góc của điểm B lên mặt phẳng (ABC) trùng với trọng tâm tam giác ABC. Thể tích của khối tứ diện A.ABC tính theo a bằng
Đọc tiếp
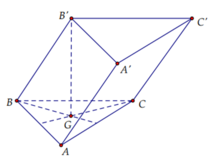
Cho hình lăng trụ tam giác ABC. A'B'C' có BB' = a, góc giữa đường thẳn BB' và mặt phẳng (ABC) bằng 60 o , tam giác ABC vuông tại C và B A C ^ = 60 o . Hình chiếu vuông góc của điểm B' lên mặt phẳng (ABC) trùng với trọng tâm tam giác ABC. Thể tích của khối tứ diện A'.ABC tính theo a bằng
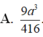
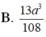
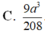
Cho tam giác ABC có các góc ∠ A = 60 o , B = 30 o . So sánh các cạnh của tam giác:
A. AB > AC > BC
B. AB > BC > CA
C. BC > AC > AB
D. CB > AB > AC
Ta có ∠C = 180o - 60o - 30o = 90o
Vì ∠C > ∠A > ∠B ⇒ AB > BC > AC. Chọn C
Đúng 0
Bình luận (0)
Cho tam giác ABC có A ^ = 60 o . Vẽ ra phía ngoài của của tam giác hai tam giác đều AMB và ANC
A. Ba điểm M,A,N thẳng hàng
B. BN = CM
C. Cả A,B đều sai
D. Cả A,B đều đúng
Cho tam giác ABC có
A
^
B
^
C
^
60
o
. Khi đó A.
Δ
ABC là tam giác nhọn B.
Δ
ABC là tam giác cân C.
Δ
ABC là tam giác đều D. Cả A,B,C đều đúng
Đọc tiếp
Cho tam giác ABC có A ^ = B ^ = C ^ = 60 o . Khi đó
A. Δ ABC là tam giác nhọn
B. Δ ABC là tam giác cân
C. Δ ABC là tam giác đều
D. Cả A,B,C đều đúng
Cho tam giác ABC có góc A = 60o, BC = 6. Tính bán kính đường tròn ngoại tiếp tam giác đó
Áp dụng định lý Sin trong tam giác ABC ta có:
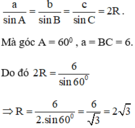
Vậy bán kính đường tròn ngoại tiếp tam giác bằng 2√3.
Đúng 0
Bình luận (0)
Trong tam giác ABC có ∠ A = 30 o , ∠ B = 60 o . Trực tâm tam giác ABC là:
A. Điểm A
B. Điểm B
C. Điểm C
D. Điểm khác A, B, C
Ta có ∠C = 180o - 30o - 60o = 90o
Tam giác ABC vuông tại C nên trực tâm tan giác ABC là điểm C.
Chọn C
Đúng 0
Bình luận (0)
Cho tứ giác ABCD có \(\widehat{B}\)=120o,\(\widehat{C}\)=60o,\(\widehat{D}\)=90o.Tính góc A và góc ngoài tại đỉnh A
giúp mik nhe
- Xét tứ giác ABCD:
\(\hat{A}+\hat{B}+\hat{C}+\hat{D}=360\text{°}\)
\(\Rightarrow\hat{A}+120\text{°}+60\text{°}+90\text{°}=360\text{°}\)
\(\Rightarrow\hat{A}=90\text{°}\)
Góc ngoài của đỉnh A \(=360\text{°}-90\text{°}=270\text{°}\)
Đúng 0
Bình luận (0)
Cho tam giác ABC có
A
^
60
o
,
B
^
1
2
C
^
. Tính
B
^
và
C
^
? A.
B
^
70
°
,
C
^
50...
Đọc tiếp
Cho tam giác ABC có A ^ = 60 o , B ^ = 1 2 C ^ . Tính B ^ và C ^ ?
A. B ^ = 70 ° , C ^ = 50 °
B. B ^ = 30 ° , C ^ = 60 °
C. B ^ = 40 ° , C ^ = 80 °
D. B ^ = 80 ° , C ^ = 40 °
LA
4 tháng 8 2021 lúc 17:55
cho tứ giác BCDE có \(\widehat{B}\)=120o và \(\widehat{E}\)=60o. Tính \(\widehat{D}\)và \(\widehat{C}\)
Đề thiếu dữ kiện bạn nhé, chỉ tính được tổng của góc D và góc C thôi.
Đúng 1
Bình luận (0)