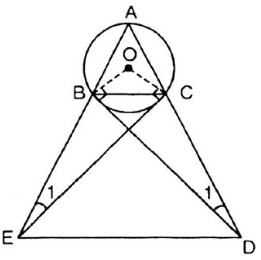
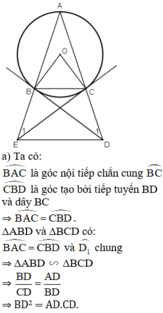
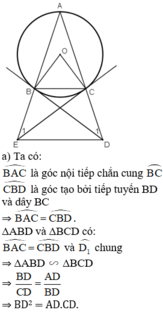
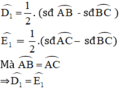cho tam giác ABC cân tại A có cạnh đáy nhỏ hơn cạnh bên nội tiếp (O;R)tiếp tuyến tại B và C của (O;R) cắt nhau tại D.
a) Chứng minh tứ giác OBDC nội tiếp
b)Đường thẳng BD và AC cắt nhau tại E. Chứng minh EB2=EC.EA
Từ điểm M trên cung nhỏ BC vẽ MI vuông góc với BC, MH vuông góc với AB, MF vuông góc với AC. Chứng minh H,I, F thẳng hàng




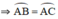
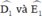 là các góc có đỉnh ở bên ngoài đường tròn nên ta có:
là các góc có đỉnh ở bên ngoài đường tròn nên ta có: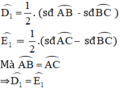

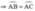
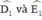 là các góc có đỉnh ở bên ngoài đường tròn nên ta có:
là các góc có đỉnh ở bên ngoài đường tròn nên ta có: