tìm nghiệm nguyên dương của phương trình 6x^2+5y^2=74
giải phương trình nghiệm nguyên dương sau:
\(6x^2+5y^2=74\)
nhanh nhanh nha mk cần gấp lứm
vì 74 và 6x^2 chia hết cho 2 nên 5y^2 chia hết cho 2 suy ra y chia hết cho 2
Ta có: \(6x^2\ge0\Rightarrow5y^2\le74\Rightarrow y^2< 15< 16\Rightarrow y< 4\)
Mà y là số nguyên dương, y chia hết cho 2 => y=2, thay vào phương trình ta có:
\(6x^2=54\Rightarrow x^2=9\Rightarrow x=3\)(vì x là số nguyên dương)
Tìm nghiệm nguyên dương của phương trình : 2xy - 6x - 5y =3041994
Tìm nghiệm nguyên của phương trình: \(x^2-xy=6x-5y-8\)
Biện pháp tu từ được sử dụng trong câu "sương vô tình đậu trên mắt rưng rưng" là sự lặp lại âm tiết "rưng rưng". Tác dụng của biện pháp này là tạo ra hiệu ứng âm thanh đặc biệt, tăng cường tính hài hòa và nhấn mạnh sự mơ hồ, mờ ảo của cảnh tượng mà câu muốn diễn tả. Ngoài ra, biện pháp tu từ còn giúp tạo ra sự nhấn mạnh, tăng cường tính cảm xúc và sự chú ý của người đọc đối với câu. có đúng khum thì ko bít nữa nhớ tick ạ
Đặt y = x + k (với k \(\inℤ\))
Khi đó ta được x2 - xy = 6x - 5y - 8
<=> x2 - x(x + k) = 6x - 5(x + k) - 8
<=> xk + x - 5k - 8 = 0
<=> (k + 1)(x - 5) = 3
Lập bảng ta có :
| x - 5 | 1 | 3 | -1 | -3 |
| k + 1 | 3 | 1 | -3 | -1 |
| x | 6 | 8 | 4 | 2 |
| k | 2 | 0 | -4 | -2 |
mà y = x + k
nên ta được các cặp (x;y) thỏa là (6 ; 8) ; (8;8) ; (4 ; 0) ; (2;0)
Tìm nghiệm nguyên dương của phương trình sau:
(2x + 5y + 1)(2|x| + y + x2 + x) = 105
Do VP là số lẻ
<=> 2x + 5y + 1 là số lẻ và \(2^{\left|x\right|}+y+x^2+x\) là số lẻ
<=> y chẵn và \(2^{\left|x\right|}+y+x\left(x+1\right)\) là số lẻ
=> \(2^{\left|x\right|}\) là số lẻ (do y chẵn và x(x+1) chẵn)
=> x = 0
PT <=> \(\left(5y+1\right)\left(1+y\right)=105\)
<=> y = 4 (thử lại -> thỏa mãn)
KL: x = 0; y = 4
tìm các cặp số nguyên dương (x,y) thoả mãn : \(6x^2+5y^2=74\)
Cuu Cần gấp !!!!![]()
Tìm nghiệm nguyên x, y của phương trình: \(x^2-xy=6x-5y-8\)
Tìm nghiệm nguyên của phương trình sau
a,x^2 -xy =6x-5y-8
b, 3x^2 -4y^2=13
a)
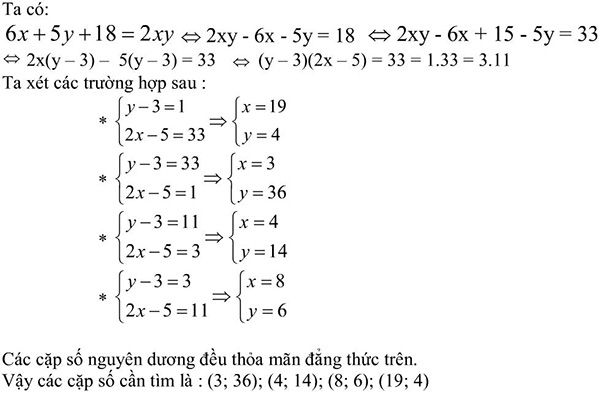
b)
Nhận thấy: x phải là số lẻ. Vì nếu x là số chẵn thì 3x^2 sẽ là số chẵn => 3x^2-4y^2 là số chẵn trong khi 13 là số lẻ
x là số lẻ => x có dạng x= 2k+1 với k thuộc Z
thay x=2k+1 vào phương trình ta có:
3(4k^2+4k+1) - 4y^2 = 13
<=> 6k^2+6k-2y^2=5
<=> 6k(k+1) = 5+2y^2
Dễ thấy vế trái là số chẵn trong khi vế phải là số lẻ => phương trình không có nghiệm nguyên => dpcm
Tìm nghiệm nguyên của phương trình :
a.x^2-xy=6x-5y-8
b.2x^2+3x^2-2y^2=7
Giải phương trình nghiệm nguyên:
a. \(3x^2-4y^2=13\)
b. \(6x^2+5y^2=74\)
c. \(x^2+x+13=y^2\)