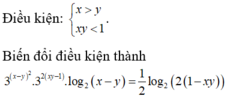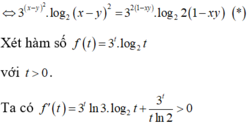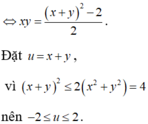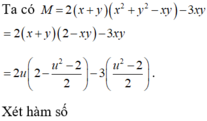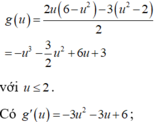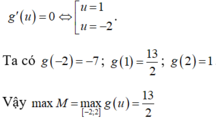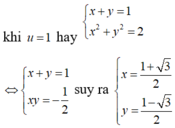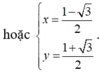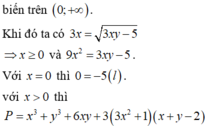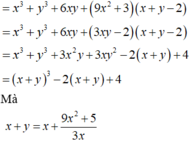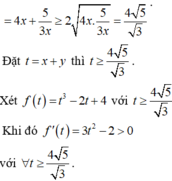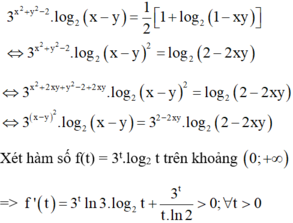Tìm các cặp số tự nhiên x,y thỏa mãn 1+x+3x2+x3=y3
TM
Những câu hỏi liên quan
Cho x , y là các số thực thỏa mãn điều kiện:
3
x
2
+
y
2
-
2
.
log
2
x
-
y...
Đọc tiếp
Cho x , y là các số thực thỏa mãn điều kiện: 3 x 2 + y 2 - 2 . log 2 x - y = 1 2 [ 1 + log 2 ( 1 - x y ) ] . Tìm giá trị lớn nhất của biểu thức M = 2 ( x 3 + y 3 ) - 3 x y .
A. 3
B. 7
C. 17 2
D. 13 2
Cho hai số thực x,y thỏa mãn:
9
x
3
+
(
2
-
y
3
x
y
-
5
)
x
+
3
x
y
-...
Đọc tiếp
Cho hai số thực x,y thỏa mãn: 9 x 3 + ( 2 - y 3 x y - 5 ) x + 3 x y - 5 = 0 . Tìm giá trị nhỏ nhất của P = x 3 + y 3 + 6 x y + 3 ( 3 x 2 + 1 ) ( x + y - 2 )
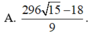
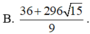
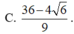
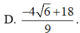
Cho x, y là các số thực thỏa mãn điều kiện
3
x
2
+
y
2
-
2
.
log
2
x
-
y
1
2
1
+
log...
Đọc tiếp
Cho x, y là các số thực thỏa mãn điều kiện 3 x 2 + y 2 - 2 . log 2 x - y = 1 2 1 + log 2 1 - x y . Tìm giá trị lớn nhất của biểu thức M = 2(x3 + y3) – xy.
A. 7
B. 13 2
C. 17 2
D. 3
Cho x,yÎR thỏa mãn:
3
x
2
+
y
2
-
2
.
l
o
g
2
(
x
-
y
)
1
2
1
+
log
2...
Đọc tiếp
Cho x,yÎR thỏa mãn: 3 x 2 + y 2 - 2 . l o g 2 ( x - y ) = 1 2 1 + log 2 1 - x y . Tìm giá trị lớn nhất của M = 2 ( x 3 + y 3 ) - 3 x y .
A. 13 2
B. 17 2
C. 3
D. 7
1.Cho các số thực x, y thỏa mãn x+y+4=0. Tìm GTLN của biểu thức: A= 2(x3+y3)+3(x2+y2)+10xy
số cásố các cặp số tự nhiên (x;y) thỏa mãn (x-y)(x+y)=2014 làc cặp số tự nhiên (x;y) thỏa mãn (x-y)(x+y)=2014 là...
a) Tìm x,y thỏa mãn x3+y3 +1=3xy tính P= (1+1/x)(1+1/y)(x+y)
b) Cho a+2b+c=0 Tính P= a2/2ab + 4b2/ac + c2/2ab
c) Cho x,y Thỏa mãn x3+y3+8=6xy Tính P=(1 + z/y)(1 + z/x)(x+y)
giúp mik với ạ cảm ơn nhiều nhiều!!!
Tìm tất cả các cặp số nguyên ( x,y ) thỏa mãn
x3 - x2y + x + 3y + 1 = 0
Lời giải:
PT $\Leftrightarrow x^3+x+1-y(x^2-3)=0$
$\Leftrightarrow y=\frac{x^3+x+1}{x^2-3}$ (hiển nhiên $x^2-3\neq 0$ với mọi $x$ nguyên)
Để $y$ nguyên thì $\frac{x^3+x+1}{x^2-3}$ nguyên
$\Leftrightarrow x^3+x+1\vdots x^2-3$
$\Rightarrow x(x^2-3)+4x+1\vdots x^2-3$
$\Rightarrow 4x+1\vdots x^2-3$
Hiển nhiên $4x+1\neq 0$ nên $|4x+1|\geq x^2-3$
Nếu $x\geq \frac{-1}{4}$ thì $4x+1\geq x^2-3$
$\Leftrightarrow x^2-4x-4\leq 0$
$\Leftrightarrow (x-2)^2\leq 8<9$
$\Rightarrow -3< x-2< 3$
$\Rightarrow -1< x< 5$
$\Rightarrow x\in \left\{0; 1; 2; 3; 4\right\}$.
Nếu $x< \frac{-1}{4}$ thì $-4x-1\geq x^2-3$
$\Leftrightarrow x^2+4x-2\leq 0$
$\Leftrightarrow (x+2)^2-6\leq 0$
$\Leftrightarrow (x+2)^2\leq 6< 9$
$\Rightarrow -3< x+2< 3$
$\Rightarrow -5< x< 1$
$\Rightarrow x\in\left\{-4; -3; -2; -1\right\}$
Đến đây bạn thay vào tìm $y$ thôi
Đúng 0
Bình luận (0)
Trong các cặp số tự nhiên x;y thỏa mãn (2x+1)(y-3)=10. tìm x;y lớn nhất
Trong các cặp số tự nhiên (x;y)thỏa mãn (2x+1).(y-3)cặp số thỏa mạn x;y?