Cho tam giác ABC có 3 góc nhọn. 3 đường cao AA', BB', CC' cắt nhau tại H; A1, B1, C1 là các điểm đối xứng của H qua BC, AC,AB. CM: \(\dfrac{AA_1}{AA'}+\dfrac{BB_1}{BB'}+\dfrac{CC_1}{CC'}\) không đổi
BB
Những câu hỏi liên quan
cho tam giác nhọn abc và 3 đường cao aa' , bb', cc' cắt nhau tại h . Biết ah/aa'=bh/bb'=ch/cc' . CMR tam giác abc là tam giác đều
Ai giúp mik với !!!!!!!!!!
cho tam giác ABC cả 3 góc đều nhọn các đường cao AA';BB';CC' cắt nhau tại H
cm
\(\frac{A'H}{AA'}+\frac{B'H}{BB'}+\frac{C'H}{CC'}=1\)
đề đúng rồi nè
Cho tam giác ABC nhọn. Các đường cao AA’, BB’, CC’ cắt nhau tại H. Tổng
H
A
A
A
+
H
B
B
B
+
H
C
C
C...
Đọc tiếp
Cho tam giác ABC nhọn. Các đường cao AA’, BB’, CC’ cắt nhau tại H. Tổng H A ' A A ' + H B ' B B ' + H C ' C C ' bằng?
cho tam giác ABC nhọn có các đường cao AA',BB',CC' cắt nhau tại H. tính giá trị biểu thức M=\(\frac{AH}{AA'}+\frac{BH}{BB'}+\frac{CH}{CC'}\)
Ta có : \(\frac{AH}{AA'}=\frac{S_{ABH}}{S_{ABA'}}=\frac{S_{ACH}}{S_{ACA'}}=\frac{S_{ABH}+S_{ACH}}{S_{ABC}}\) ( Tính chất dãy tỉ số bằng nhau, tỉ số diện tích )
Tương tự ta có :
\(\frac{BH}{BB'}=\frac{S_{AHB}+S_{BHC}}{S_{ABC}}\) , \(\frac{CH}{CC'}=\frac{S_{ACH}+S_{BHC}}{S_{SBC}}\)
Do đó :
\(\frac{AH}{AA'}+\frac{BH}{BB'}+\frac{CH}{CC'}=\frac{2\left(S_{ABH}+S_{AHC}+S_{BHC}\right)}{S_{ABC}}=\frac{2\cdot S_{ABC}}{S_{ABC}}=2\)
Vậy : \(\frac{AH}{AA'}+\frac{BH}{BB'}+\frac{CH}{CC'}=2\)
cho tam giác ABC có các đường cao AA', BB', CC' cắt nhau tại H. Biết AH/AA'=BH/BB'-CH/CC'. CMR: Tam giác ABC đều
cho tam giác ABC có các đường cao AA', BB', CC' cắt nhau tại H. Biết AH/AA'=BH/BB'-CH/CC'. CMR: Tam giác ABC đều
Cho tam giác nhọn ABC, 3 đường cao AA', BB', CC' cắt nhau tại H. C/m: H là tâm đường tròn nội tiếp ΔA'B'C'
Cho tam giác ABC, 3 đường cao AA',BB',CC' cắt nhau tại H. Chứng minh HA'/AA'+HB'/BB'+HC'/CC' = 1
Xem chi tiết
Cho tam giác nhọn ABC, các đường cao AA, BB, CC cắt nhau tại H. Chứng minh rằng:
H
A
A
A
+
H
B
B
B
+
H
C
C
C
1
Đọc tiếp
Cho tam giác nhọn ABC, các đường cao AA', BB', CC' cắt nhau tại H. Chứng minh rằng: H A ' A A ' + H B ' B B ' + H C ' C C ' = 1
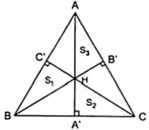
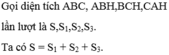
+ Các tam giác ABC và ABH có chung đáy AB nên tỉ số đường cao bằng tỉ số diện tích: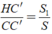
+ Tương tự: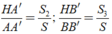
Khi đó ta có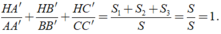
Đúng 0
Bình luận (0)

