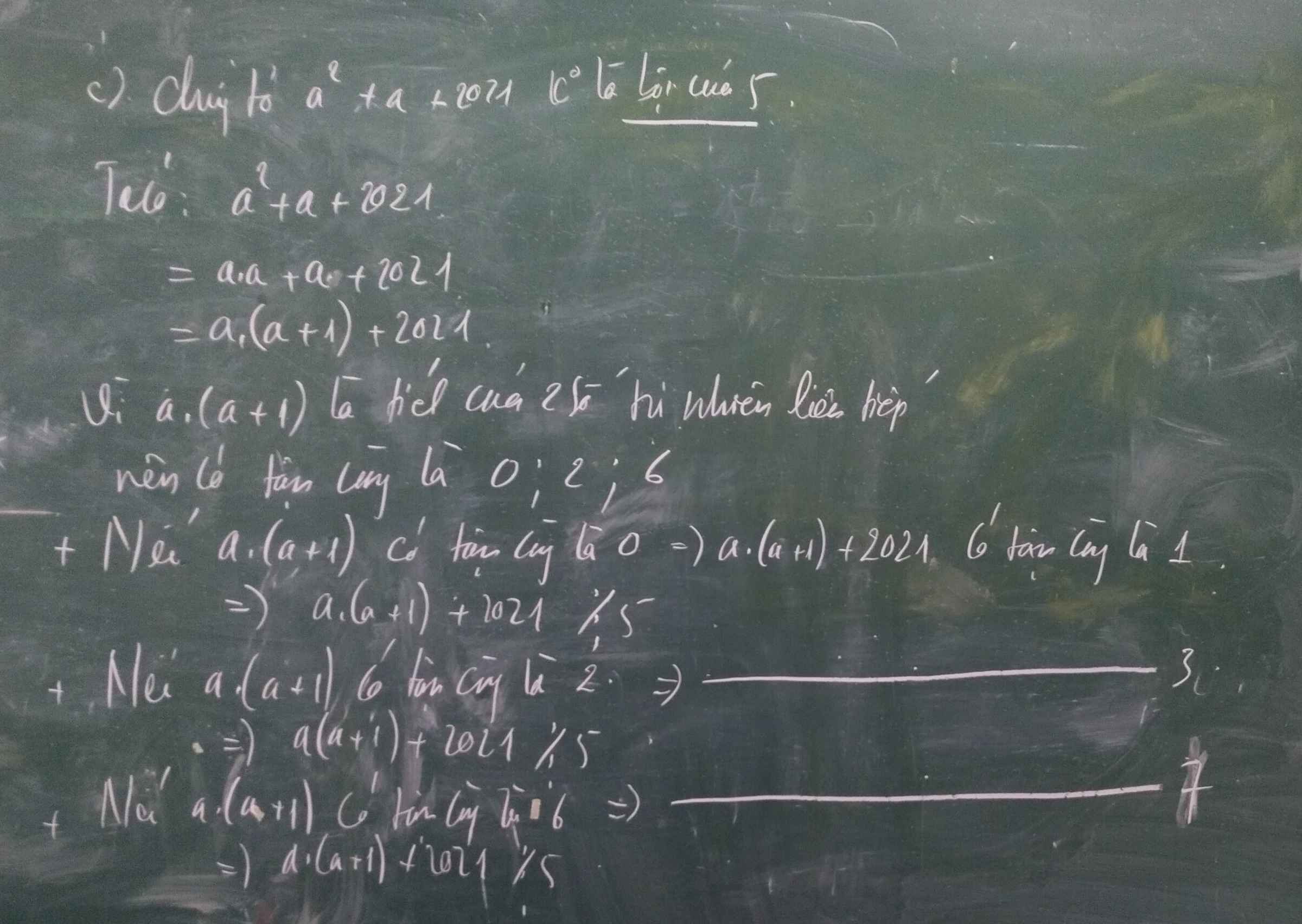chứng tỏ a^2 + a + 2021 không là bội của 5
HB
Những câu hỏi liên quan
Cho A thuộc bội con N, chứng tỏ rằng a^2+a+2021 không là bội của 5
a thuộc N nên a có dạng 5k,5k+1,5k+2,5k+3,5k+4
với a=5k thì a^2 và a chia hết cho 5 mà 2021 ko chia hết nên tổng ko chia hết
với a=5k+1 =>a2+a+2021=(5k+1)2+5k+1+2021=25k2+15k+2023 không chia hết cho 5
bạn làm tương tự với mấy cây còn lại, ko đc thì nói nhé
chúc bạn học tốt
NNBC-1/1/2022
Cho a ∈ N, chứng tỏ rằng a2 + a + 2021 không là bội của 5
Cho a ∈ N, chứng tỏ rằng a^2+ a + 2021 không là bội của 5
\(a^2+a+2021=a\left(a+1\right)+2021\)
a và (a+1) là hai số TN liên tiếp => tích a(a+1) có chữ số tận cùng = {0;2;6}
=> a(a+1)+2021 có chữ số tận cùng = {1;3;7}\(\Rightarrow a^2+a+2021\) không chia hết cho 5 nên nó không phải bội của 5
a) chứng tỏ rằng: số aaaaaa là bội của 37037
b) chứng tỏ rằng: giá trị của biểu thức
B=\(3+3^3+3^5+3^7+...+3^{2017}+3^{2019}+3^{2021}\) là bội của 273
a) \(\overline{aaaaaa}=a.111111=a.3.37037\) \(⋮\)\(37037\)
b) Nhận thấy các hạng tử trong B đều chia hết cho 3 => B chia hết cho 3
\(B=3+3^3+3^5+3^7+...+3^{2017}+3^{2019}+3^{2021}\)
\(=\left(3+3^3+3^5\right)+\left(3^7+3^9+3^{11}\right)+....+\left(3^{2017}+3^{2019}+3^{2021}\right)\)
\(=3\left(1+3^2+3^4\right)+3^7\left(1+3^2+3^4\right)+...+3^{2017}\left(1+3^2+3^4\right)\)
\(=\left(1+3^2+3^4\right)\left(3+3^7+...+3^{2017}\right)\)
\(=91\left(3+3^7+....+3^{2017}\right)\)\(⋮\)\(91\)
mà (3;91) = 1
=> B chia hết cho 273
Đúng 0
Bình luận (0)
B chia hết cho 273
Còn câu a thì mình không biết nhé, xin lỗi bạn.
Đúng 0
Bình luận (0)
Chứng tỏ rằng
a, (a+2021).(a+2020) là bội của 2 với mọi số tự nhiên a
ta có a+2021 và a+2020 là hai số tự nhiên liên tiếp
nên chắc chắc có 1 số chẵn trong hai số đó
vậy tích (a+2021)(a+2020) là số chẵn, hay là bội của 2
chứng minh: a^2+a+2021 không là bội của 5
giúp mik
Ta có :
a²+a+2021
= a.a+a+2021
= a.(a+1)+2021
Ví a.(a+1) là tích hai số liên tiếp nên có tân cùng là 0;1;2;6
⇒ a.(a+1)+2021 có tân cùng là 1;2;3;7 và không chia hết cho 5
Vậy a²+a+2021 không chia hết cho 5
Đúng 1
Bình luận (0)
cho a=2022/2021^2+1 + 2022/2021^2+2 + 2022/2021^2+3 + ....+2022/2021^2+2021 Hãy chứng tỏ A không phải là số tự nhiên
Ta có: \(\frac{2022}{2021^2+k}\le\frac{2022}{2021^2}\) (với \(k\)là số tự nhiên bất kì)
Ta có:
\(A=\frac{2022}{2021^2+1}+\frac{2022}{2021^2+2}+...+\frac{2022}{2021^2+2021}\)
\(\le\frac{2022}{2021^2}+\frac{2022}{2021^2}+...+\frac{2022}{2021^2}=\frac{2022}{2021^2}.2021=\frac{2022}{2021}\)
Ta có: \(\frac{2022}{2021^2+k}>\frac{2022}{2021^2+2021}=\frac{2022}{2021.2022}=\frac{1}{2021}\)với \(k\)tự nhiên, \(k< 2021\))
Suy ra \(A=\frac{2022}{2021^2+1}+\frac{2022}{2021^2+2}+...+\frac{2022}{2021^2+2021}\)
\(>\frac{1}{2021}+\frac{1}{2021}+...+\frac{1}{2021}=\frac{2021}{2021}=1\)
Suy ra \(1< A\le\frac{2022}{2021}\)do đó \(A\)không phải là số tự nhiên.
Ta có: (với là số tự nhiên bất kì)
Ta có:
Ta có:
Đúng 0
Bình luận (0)
Ta có: (với là số tự nhiên bất kì)
Ta có:
Ta có:
Đúng 0
Bình luận (0)
cho a=2022/2021^2+1 + 2022/2021^2+2 + 2022/2021^2+3 + ....+2022/2021^2+2021 Hãy chứng tỏ A không phải là số tự nhiên
Ta có: \(\frac{2022}{2021^2+k}\le\frac{2022}{2021^2}\) (với \(k\)là số tự nhiên bất kì)
Ta có:
\(A=\frac{2022}{2021^2+1}+\frac{2022}{2021^2+2}+...+\frac{2022}{2021^2+2021}\)
\(\le\frac{2022}{2021^2}+\frac{2022}{2021^2}+...+\frac{2022}{2021^2}=\frac{2022}{2021^2}.2021=\frac{2022}{2021}\)
Ta có: \(\frac{2022}{2021^2+k}>\frac{2022}{2021^2+2021}=\frac{2022}{2021.2022}=\frac{1}{2021}\)với \(k\)tự nhiên, \(k< 2021\))
Suy ra \(A=\frac{2022}{2021^2+1}+\frac{2022}{2021^2+2}+...+\frac{2022}{2021^2+2021}\)
\(>\frac{1}{2021}+\frac{1}{2021}+...+\frac{1}{2021}=\frac{2021}{2021}=1\)
Suy ra \(1< A\le\frac{2022}{2021}\)do đó \(A\)không phải là số tự nhiên.