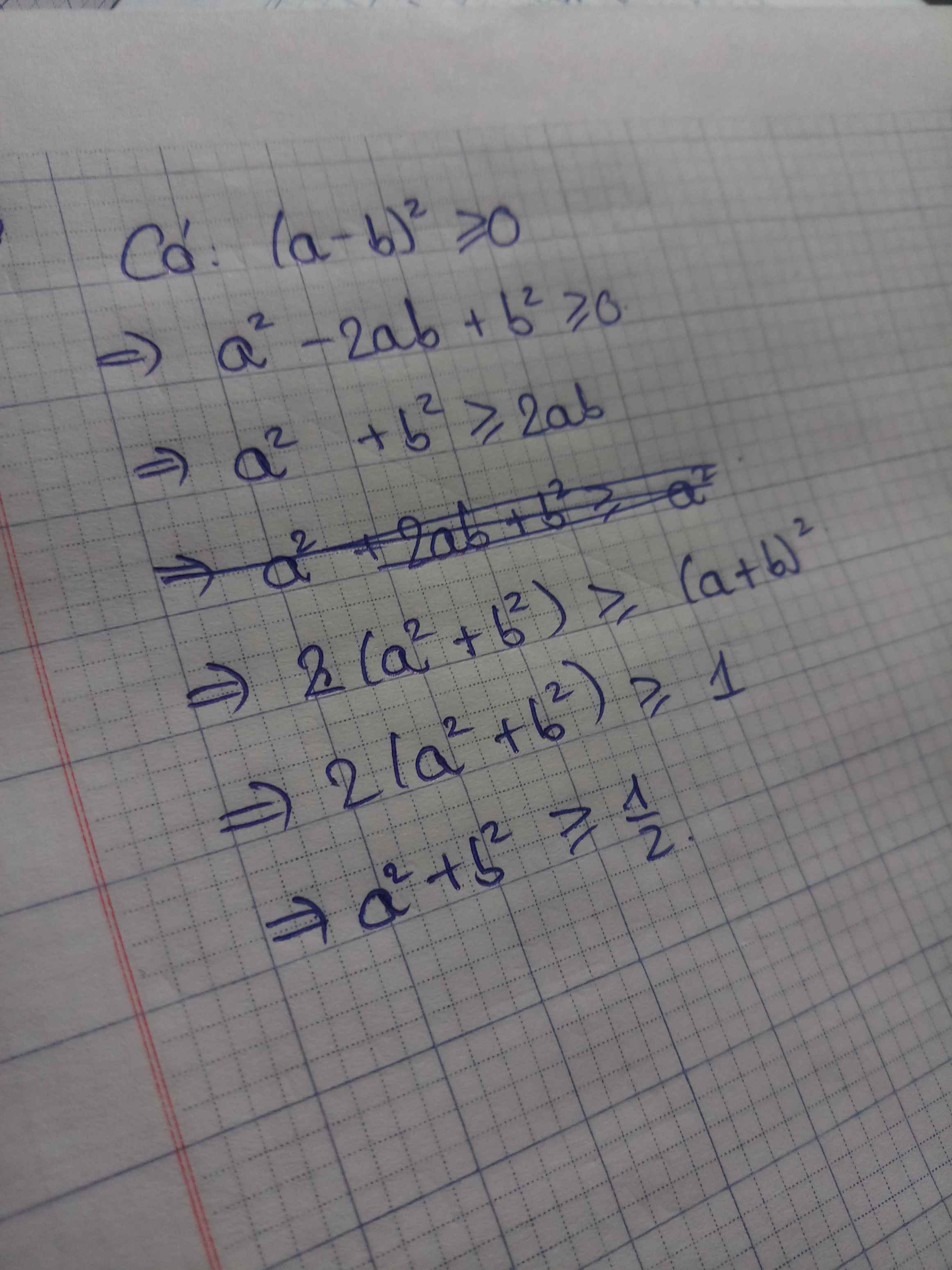chứng minh rằng: nếu (a,b)=1 thì (a^2, a+b)=1
VN
Những câu hỏi liên quan
chứng minh rằng nếu a+b=1 thì a^2+b^2>=1/2
1)chứng minh rằng nếu a+b+c=1 thì a^4 +c^4 +b^4 =abc
2) với a,b,c dương chứng minh rằng 2căna +2cănb+2cănc +a^2+b^2+c^2 >= 3(a+b+c)
mk chẳng biết nguyen hoang phi hung ak
Đúng 0
Bình luận (0)
Chứng minh rằng :Nếu (a;b) = 1 thì (a2; a+b) = 1
Lời giải:
Giả sử $a^2,a+b$ không nguyên tố cùng nhau.
Gọi $p$ là ước nguyên tố chung lớn nhất của $a^2,a+b$.
$\Rightarrow a^2\vdots p; a+b\vdots p$
$\Rightarrow a\vdots p; a+b\vdots p$
$\Rightarrow (a+b)-a\vdots p\Rightarrow b\vdots p$
Vậy $p$ là ước chung của $a,b$. Mà $(a,b)=1$ nên $p=1$ (vô lý do $p$ là ước nguyên tố)
Vậy điều giả sử là sai. Tức là $(a^2, a+b)=1$
Đúng 0
Bình luận (0)
chứng minh rằng nếu:1/a+1/b+1/c=2 và a+b+c=a*b*c thì 1/a^2+1/b^2+1/c^2=3
(a + b + c)² = a² + b² + c² + 2ab + 2bc + 2ac.
(1/a + 1/b + 1/c)² = 1/a² + 1/b² + 1/c² + 2(1/ab + 1/bc + 1/ac) = 4
<=> 1/a² + 1/b² + 1/c² + 2(bcac + abac + abbc)/(a²b²c²) = 4
<=> 1/a² + 1/b² + 1/c² + 2abc(a + b + c)/(a²b²c²) = 4
<=> 1/a² + 1/b² + 1/c² + 2 = 4
(vi` abc(a + b + c) = a² b² c²)
<=> 1/a² + 1/b² + 1/c² = 2 !!
Đúng 0
Bình luận (0)
Chứng minh rằng nếu a^2 - b^2 là 1 số NT thì a^2 - b^2 = a + b
cho a,b,c là các số thực thỏa man: a+\(\dfrac{1}{b}=b+\dfrac{1}{c}=c+\dfrac{1}{a\backslash}\).
a) chứng minh nếu a,b,c đôi một khác nhau thì a2b2c2=1
b) chứng minh rằng nếu a,b,c>0 thì a=b=c
chứng minh rằng nếu (a-b).(a+b+1)=b^2 thì a-b và a+b+1 đều là số chính phương
Chứng minh rằng nếu (a-b)(a+b+1)=b^2 thì a-b và a+b+1 đều là số chính phương.
Chứng minh rằng nếu a + b = 1 t h ì a 2 + b 2 ≥ 1 / 2
Ta có: a + b = 1 ⇔ b = 1 – a
Thay vào bất đẳng thức a2 + b2 ≥ 1/2 , ta được:
a2 + (1 – a)2 ≥ 1/2 ⇔ a2 + 1 – 2a + a2 ≥ 1/2
⇔ 2a2 – 2a + 1 ≥ 1/2 ⇔ 4a2 – 4a + 2 ≥ 1
⇔ 4a2 – 4a + 1 ≥ 0 ⇔ (2a – 1)2 ≥ 0 (luôn đúng)
Vậy bất đẳng thức được chứng minh
Đúng 0
Bình luận (0)