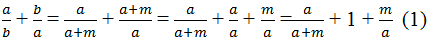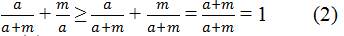Bài toán: Chứng minh rằng tổng của một phân số dương với số nghịch đảo của nó thì không nhỏ hơn 2
MT
Những câu hỏi liên quan
Bài 101*:
Chứng minh rằng tổng của một phân số dương với số nghịch đảo của nó thì không nhỏ hơn 2
Chứng minh rằng tổng của một phân số dương với số nghịch đảo của nó thì không nhỏ hơn 2.
Gọi a/b với a > 0, b > 0 là phân số đã cho và b/a là phân số nghịch đảo của nó . Không mất tính tổng quát giả sử 0 < a ≤ b.
Đặt b = a + m (m ∈ Z, m ≥ 0)
Ta có:
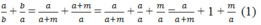
Và 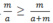 (dấu "=" xảy ra khi m = 0)
(dấu "=" xảy ra khi m = 0)
Suy ra: 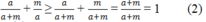
Từ (1) và (2) suy ra:
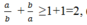 , (dấu "=" xảy ra khi m = 0 hay a = b )
, (dấu "=" xảy ra khi m = 0 hay a = b )
Đúng 0
Bình luận (0)
Chứng minh rằng tổng của một phân số dương với số nghịch đảo của nó thì không nhỏ hơn 2
Giả sử phân số và nghịch đảo của nó là: \(\frac{a}{b};\frac{b}{a}\)
Do phân số dương nên( a;b) cùng dấu hay a.b>0
Ta có:
\(\frac{a}{b}+\frac{b}{a}-2=\frac{a^2+b^2-2ab}{ab}=\frac{\left(a-b\right)^2}{ab}\ge0\)
Do đó: \(\frac{a}{b}+\frac{b}{a}\ge2\)
Đúng 0
Bình luận (0)
Chứng minh rằng tổng của một phân số dương với số nghịch đảo của nó thì không nhỏ hơn 2 ?
Gọi phân số dương là \(\dfrac{a}{b}\) . ( Không mất tính tổng quát )
Cho \(a>0,\) \(b>0\) và \(a\ge b\) . Ta có thể viết \(a=b+m\left(m\ge0\right)\) .
Ta có:
\(\dfrac{a}{b}+\dfrac{b}{a}=\dfrac{b+m}{b}+\dfrac{b}{b+m}=1+\dfrac{m}{b}\ge1+\dfrac{m}{b+m}+\dfrac{b}{b+m}=1+\dfrac{m+b}{b+m}=2\)\(\Rightarrow\dfrac{a}{b}+\dfrac{b}{a}\ge2\)
Dấu đẳng thức xảy ra khi \(a=b\left(m=0\right)\)
Đúng 0
Bình luận (0)
Gọi a/b với a > 0, b > 0 là phân số đã cho và b/a là phân số nghịch đảo của nó . Không mất tính tổng quát giả sử 0 < a ≤ b.
Đặt b = a + m (m ∈ Z, m ≥ 0)
Ta có:
Và 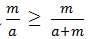
Suy ra:
Từ (1) và (2) suy ra:
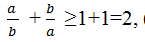
Đúng 0
Bình luận (0)
chứng minh rằng tổng của một phân số dương với số nghịch đảo của nó thì không nhỏ hơn 2?
Gọi phân số đó là a/b (ĐK: a,b # 0, a và b cùng dấu )
a/b + b/a ≥ 2 <=> (a² + b ²)/ab ≥ 2
<=> a² - 2ab + b² ≥ 0
<=> ( a – b )² ≥ 0 ( Luôn đúng với mọi a, b)
=> Đpcm
Đúng 0
Bình luận (2)
mk giải đc nè, tick mk nha!!
Gọi phân số dương là a/b. Ko mất tính tổng quát, giả sử như: a>0, b>0 và a > b. Ta có thể viết a=b+m ( m > 0). Ta có:
a/b+b/a=b+m/b+b/m+b=1+m/b+b/b+m > 1+ m/b+m+b/b+m=1+m+b/b+m=2.
Vậy a/b+b/a > 2.
Đúng 0
Bình luận (2)
Gọi phân số dương là a/b. Không mất tính tổng quát, giả sử a>0, b>0 và a\(\ge\)b. Ta có thể viết a=b+m (m\(\ge\)0). Ta có:
(a/b)+(b/a)=b/(b+m)\(\ge\)1+[m/(b+m)]+[b/(b+m)]=1+[(m+b)/(b+m)]=2.
Vậy (a/b)+(b/a)=2
Dấu đẳng thức xảy ra khi a=b (m=0).
Đúng 0
Bình luận (0)
chứng minh rằng tổng của một phân số dương với số nghịch đảo của nó thì không nhỏ hơn hai ?
Giả sử phân số và nghịch đảo của nó là \(\frac{a}{b};\frac{b}{a}\)
Do phân số dương nên \(a;b\)cùng dấu hay \(a.b>0\)
Ta có \(\frac{a}{b}+\frac{b}{a}-2=\frac{a^2+b^2-2ab}{ab}=\frac{\left(a-b\right)^2}{ab}\ge0\)
Do đó \(\frac{a}{b}+\frac{b}{a}\ge2\)
Đúng 0
Bình luận (0)
Gọi phân số dương là \(\frac{a_1}{a_2}\). Không mất tính tổng quát, giả sử \(a_1\ge a_2>0\). Ta có thể viết \(a_1=a_2+m\)\(\left(m\inℕ\right)\). Ta có:
\(\frac{a_1}{a_2}+\frac{a_2}{a_1}=\frac{a_2+m}{a_2}+\frac{a_2}{a_2+m}=1+\frac{m}{a_2}+\frac{a_2}{a_2+m}\ge1+\frac{m}{a_2+m}+\frac{a_2}{a_2+m}=1+\frac{m+a_2}{a_2+m}=2\)
Vậy \(\frac{a_1}{a_2}+\frac{a_2}{a_1}\ge2\).
Dấu đẳng thức xảy ra khi \(a_1=a_2\)\(\left(m=0\right)\).
Chứng minh rằng tổng của một phân số dương với số nghịch đảo của nó thì không nhỏ hơn 2.
Ta gọi phân số đó là \(\frac{a}{b}\) ,vì phân số dương\(\Rightarrow a.b=\)dương .
Ta chúng minh \(\frac{a}{b}+\frac{b}{a}\ge2\)
\(\frac{a}{b}+\frac{b}{a}=\frac{a^2+b^2}{ab}=\frac{a^2-ab-ab+b^2}{ab}+2=\frac{a\left(a-b\right)-b\left(a-b\right)+2}{ab}\)
\(=\frac{\left(a-b\right)^2}{ab}+2\ge2\)
Vì :
\(\left(a-b\right)^2\ge0\) và \(ab>0\)
\(\Rightarrow\)Phân số không âm .
\(\Rightarrow\)Tổng không bé hơn 2
Đúng 0
Bình luận (0)
a)Chứng minh rằng tổng của một phân số dương với nghịch đảo của nó không nhỏ hơn 2.
b) Tìm các phân số có tử và mẫu đều dương sao cho tổng của phân số đó với nghịch đảo của nó có giá trị nhỏ nhất.
a. Gọi phân số cần tìm là \(\frac{a}{b}\)
\(\Rightarrow\) Phân số nghịch đảo là \(\frac{b}{a}\)
Theo bài ra, ta có:
\(\frac{a}{b}+\frac{b}{a}\ge2\)
\(\Leftrightarrow\frac{a^2+b^2}{ab}\ge2\)
\(\Leftrightarrow a^2+b^2\ge2ab\)
\(\Leftrightarrow a^2+b^2-2ab\ge0\)
\(\Leftrightarrow a^2-ab+b^2-ab\ge0\)
\(\Leftrightarrow a\left(a-b\right)+b\left(b-a\right)\ge0\)
\(\Leftrightarrow a\left(a-b\right)-b\left(a-b\right)\ge0\)
\(\Leftrightarrow\left(a-b\right)\left(a-b\right)\ge0\)
\(\Leftrightarrow\left(a-b\right)^2\ge0\)
Vì (a-b)2 chắc chắn lớn hơn hoặc bằng 0
\(\Rightarrow\frac{a}{b}+\frac{b}{a}\ge2\)
Vậy tổng của một phân số dương với ghịch đảo của nó luôn lớn hơn hoặc bằng 2.
Đúng 0
Bình luận (0)
Chứng minh rằng tổng của một phân số dương với số nghịch đảo của nó không nhỏ hơn 2
gọi p/s đó là a/b (a;b \(\in\) Z,b \(\ne\) 0)
Ta cần c/m \(\frac{a}{b}+\frac{b}{a}\ge2\)
Nhân cả 2 vế cho ab,ta đc:
\(\left(\frac{a}{b}+\frac{b}{a}\right).ab\ge2ab\)
\(\Leftrightarrow\frac{a^2b}{b}+\frac{b^2a}{a}\ge2ab\Leftrightarrow a^2+b^2\ge2ab\)
\(\Leftrightarrow a^2+b^2-2ab\ge0\Leftrightarrow\left(a-b\right)^2\ge0\) (dấu "=" xảy ra <=>a=b0
BĐT cuối luôn đúng,ta có đpcm
Đúng 0
Bình luận (0)
Gọi phân số dương là \(\frac{a}{b}\).Không mất tích tổng quát giả sử a>0,b>0 và a\(\ge\) b.Ta có thể viết a=b+m(m\(\ge\) 0).Ta có;
\(\frac{a}{b}+\frac{b}{a}=\frac{b+m}{b}+\frac{b}{m+b}\)
=\(1+\frac{m}{b}+\frac{b}{m+b}\ge1+\frac{m}{b+m}+\frac{b}{b+m}\)
=\(1+\frac{m+b}{b+m}=2\)
Vậy \(\frac{a}{b}+\frac{b}{a}\ge2\)
Đúng 0
Bình luận (0)
Gọi p/s đó là : a/b ( vs mọi a:b \(\in\) N* )
Theo bài ra ta có :
a/b + b/a = \(\frac{2a+2b}{ab}\) = \(\frac{2\left(a+b\right)}{ab}\)
Vậy tổng của một phân số dương với số nghịch đảo của nó không nhỏ hơn 2
Đúng 0
Bình luận (0)
Xem thêm câu trả lời