dãy số dc tìm ra trong kim tự tháp ai cập là gì
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
NG
Những câu hỏi liên quan
Đến nay, người ta tìm ra 138 kim tự tháp ở Ai Cập. Tất cả đều được xây ở tả ngạn sông Nile, dòng sông dài nhất thế giới với hơn 6 nghìn km. Kim tự tháp Ai Cập. Trong số các kim tự tháp ở Ai Cập, Kheops chính là công trình kỳ vĩ nhất với chiều cao lên tới 146 m, chiều dài đáy là 227,7 m.
Mình trả lời đúng về kim tự tháp chưa ?
Xem chi tiết
Đến nay, người ta tìm ra 138 kim tự tháp ở Ai Cập. Tất cả đều được xây ở tả ngạn sông Nile, dòng sông dài nhất thế giới với hơn 6 nghìn km. Kim tự tháp Ai Cập. Trong số các kim tự tháp ở Ai Cập, Kheops chính là công trình kỳ vĩ nhất với chiều cao lên tới 146 m, chiều dài đáy là 227,7 m
Xem chi tiết
Kim tự tháp Ai Cập là một trong những công trình kiến trúc cổ đại của nền văn minh Ai Cập cổ đại, công trình được xây dựng với hình chóp bằng đá với một tỷ lệ vô cùng hoàn hảo.Hiện nay tại Ai Cập có tất cả là 138 kim tự tháp theo số liệu tính đến năm 2008. Và hầu như, kim tự tháp được xem như là lăng mộ của các Pharaoh cùng hoàng hậu trong thời kỳ Cổ vương quốc và Trung vương quốc.Đặc điểm của kim tự tháp Ai Cập là có tất cả 138 kim tự tháp lớn nhỏ khác nhauĐược biết, các kim tự tháp Ai Cập đầu...
Đọc tiếp
Kim tự tháp Ai Cập là một trong những công trình kiến trúc cổ đại của nền văn minh Ai Cập cổ đại, công trình được xây dựng với hình chóp bằng đá với một tỷ lệ vô cùng hoàn hảo.
Hiện nay tại Ai Cập có tất cả là 138 kim tự tháp theo số liệu tính đến năm 2008. Và hầu như, kim tự tháp được xem như là lăng mộ của các Pharaoh cùng hoàng hậu trong thời kỳ Cổ vương quốc và Trung vương quốc.
Đặc điểm của kim tự tháp Ai Cập là có tất cả 138 kim tự tháp lớn nhỏ khác nhau
Được biết, các kim tự tháp Ai Cập đầu tiên năm ở vùng Saqqara thuộc phía Tây Bắc của Memphis. Trong đó kim tự tháp lâu đời nhất đó chính là Djoser được xây dựng vào triều đại thứ ba trong khoảng thời gian từ 2630 – 2611 TCN. Lối kiến trúc của những kim tự tháp đầu tiên này là do một kiến trúc sư là Imhotep thiết kế.
Kim tự tháp Ai Cập được xem là công trình bằng đá nguyên khối cổ nhất thế giới. Trong đó theo những nghiên cứu thì để xây được một công trình kim tự tháp thì lượng nhân công khoảng từ 20.000 – 100.000 người.
Trong toàn bộ các công trình kim tự tháp khác nhau thì tại thủ đô Cairo của Ai Cập có một công trình nổi tiếng nhất trên thế giới đó là quần thể kim tự tháp Giza. Trong đó, kim tự tháp Khufu được xem là công trình lớn nhất và được xem là kỳ quan của thế giới.
2. Lịch sử phát triển của Kim tự tháp Ai Cập2.1 Giai đoạn đầuTừ những giai đoạn đầu tiên của lịch sử Ai Cập cổ đại, thì lăng Mastaba được xem là nơi mai táng đầu tiên của người Ai Cập. Đây được xem như là kim tự tháp đầu tiên của nền văn minh này.
Kim tự tháp Ai Cập thứ 2 được nhắc đến là Djoser. Được xem là lăng mộ của Pharaoh Djoser do kiến thức sư Imhotep đích thân thiết kế và khởi công xây dựng. Qua đó mà Imhotep được xem như là một nhà kiến trúc sư đầu tiên trong lịch sử Ai Cập, và cũng là người đầu tiên phát minh ra phương pháp xây dựng chồng các Mastaba lên nhau để có thể tạo ra một công trình hình chóp với các bậc nhỏ dần từ dưới lên đến đỉnh gọi là kim tự tháp.
Qua đó mà ông đã xây dựng thành công công trình kim tự tháp như một chiếc cầu thang để linh hồn của pharaoh có thể bước lên thiên đàng. Nhờ thế mà Imhotep được người dân Ai Cập ngưỡng mộ và được thờ cúng như một vị thần.
2.2 Giai đoạn tiếpDần dần, kim tự tháp trở thành một biểu tượng quyền lực của người Ai Cập cổ đại. Việc Kim tự tháp Ai Cập được xây dựng với quy mô lớn thì cũng là lúc chế độ chuyên quyền của Pharaoh ở mức độ cao nhất. Qua đó mà các kim tự tháp lớn và nổi tiếng nhất như Giza đã được xây dựng trong giai đoạn này. Về sau, quyền lực trở nên bị phân tán dần, mức độ xây dựng cũng thu hẹp dần, không còn được cầu kỳ và chú trọng như trước nữa.
Rất lâu sau đó nữa, khi Ai Cập trong thời kỳ bị rơi vào ách thống trị của các vị vua Napata, việc xây dựng các công trình kim tự tháp Ai Cập một lần nữa phát triển ở vùng Sudan ngày nay. Qua đó, số lượng công trình ở thời đại này là khoảng 200 lăng mộ kim tự tháp lấy ý tưởng từ kim tự tháp trước đó và được xây dựng gần trung tâm vương quốc Sudan Meroe (300 TCN – 300 SCN).
2.3 Hiện NayHiện nay, các kim tự tháp Ai Cập cũng đã bị mai một dần theo thời gian cũng như trong lịch sử cho nhân vật Al-Aziz Uthman là con trai của Saladin, người đánh bại các cuộc Thập tự chinh ở nơi đây. Ông ta cố gắng phá bỏ các lăng mộ Ai Cập nhưng dường như không thể vì quy mô của nó là vô cùng lớn.
3. Ý nghĩa tượng trưng của kim tự tháp Ai CậpÝ nghĩa của kim tự tháp Ai Cập bao gồm:
3.1 Là một công trình cổ đại hùng vĩCác kim tự tháp Ai Cập cũng sẽ có những ý nghĩa tượng trưng riêng. Hình dáng của nó được coi là tượng trưng cho những mô đất nguyên thủy linh thiên mà người Ai Cập tin là trái đất được tạo ra từ vùng đất ấy cùng như là nơi mà các tia nắng chiếu xuống đầu tiên.
Bề mặt bên ngoài của Kim tự tháp được làm bằng đá vôi trắng được đánh bóng nên tạo ra một vẻ ngoài vô cùng lộng lẫy khi chung ta đứng nhìn từ xa. Ngoài ra các tên gọi của kim tự tháp cũng được đặt theo ý nghĩa có liên quan đến mặt trời như Kim tự tháp Cong tại Dahshur có nghĩa là “tỏa sáng tại phía Nam”.
Kim tự tháp có ý nghĩa gì? Biểu tượng kim tự tháp Ai Cập được xem là công trình mai táng của người Ai Cập cổ nhưng thực sự vẫn đang còn rất nhiều tranh cãi về công trình cổ đại này, người ta nhận thấy có nhiều sự bất đồng về nguyên lý thần học cụ thể cũng như chưa xác định rõ mục đích chính của việc xây dựng này. Có giả thuyết cho rằng kim tự tháp còn là một “cỗ máy hồi sinh”.
Điều này xuất phát từ tín ngưỡng xa xưa, người Ai Cập tin rằng những vì sao trên trời buổi đêm, nơi mà tất cả các ngôi sao đều xoay quanh thì đó chính là cánh cổng để lên thiên đường. Qua đó mà khi được mai táng ở vị trí đắc địa ấy thì người chết có thể dễ dàng lên được thiên đường, về với các vị thần.
Người chết trước khi lên thiên đàng sẽ có một buổi phán quyết tại “sảnh sự thật” dưới địa ngục cùng với thần Osiris và nữ Thần Maat. Dựa vào những việc mà người chết đã làm khi còn sống mà sẽ quyết định linh hồn sẽ bị đày đọa hay được sống nơi thiên đàng.
Một điểm chung đặc biệt chính là các công trình Kim tự tháp Ai Cập đều được xây dựng dọc trên tả ngạn sông Nile, nơi đây được xem là nơi mặt trời lặn và là nơi liên quan đến thế giới bên kia cửa tử.
4. Quần thể công trình kim tự tháp GizaMột trong những công trình kim tự tháp Ai Cập nổi tiếng nhất đó chính là quần thể kim tự tháp Giza. Đây được coi là một địa điểm khảo cổ trên cao nguyên Giza nằm ở ngoại ô Cairo, Ai Cập. Kim tự tháp Giza có tiếng Ả Rập là أهرامات الجيزة với nghĩa là “các kim tự tháp của Giza”.
Quần thể di tích khảo cổ này gồm 3 khu phức hợp bao gồm các kim tự tháp vĩ đại nhất cùng tượng điêu khắc Đại nhân sư, quanh đó còn có một số nghĩa trang, khu ở của công nhân cùng các khu công nghiệp. Khu quần thể di tích kim tự tháp này nằm ở sa mạc phía tây cách 9km về phía sông nile, thuộc thị trấn Giza cách trung tâm thủ đô Cairo khoảng 13km.
Qua đó, các Kim tự tháp là một biểu tượng của Ai Cập cổ đại và phổ biến, được biết đến nhiều trong nền văn minh Hy Lạp khi mà Kim Tự Tháp được đưa vào danh sách là 1 trong 7 kỳ quan của thế giới. Cho đến bây giờ, kim tự tháp Ai Cập vẫn là một biểu tượng bất diệt với thời gian là kỳ quan cổ đại duy nhất tồn tại nguyên vẹn.
Khu quần thể Kim tự tháp Giza hiện đangg thu hút rất nhiều du khách
Khu lăng mộ của quần thể Giza bao gồm Kim tự tháp Khufu, kim tự tháp Khafre, kim tự tháp Menkaure cùng với một số công trình khác cùng với đó là có thêm tượng điêu khắc đại nhân sư cao hùng vĩ. Chưa hết mà quần thể này còn có những lăng mộ hoàng gia của giới quý tộc, tăng lữ hay các quan chức cao cấp. các lăng mộ thuộc thời Vương triều mới hay các ngồi đền thờ linh thiêng bày tỏ sự kính trọng tại nơi đây.
Quần thể kim tự tháp Giza có kim tự tháp Khafre là được lưu giữ tốt nhất và hầu như nguyên vẹn nhất trong quần thể, còn giữ được lớp bóng ốp phía bên ngoài, nhất là ở trên đỉnh. Lưu ý rằng có vẻ Khafre lớn hơn kim tự tháp Khufu vò có gò đất cao hơn cũng như góc nghiêng khi xây dựng dường như cũng lớn hơn nhiều. Nhưng thực tế thì nó nhỏ hơn Khufu về trọng lượng lẫn khối lượng.
Qua đó, điểm huyền bí của Kim tự tháp Ai Cập đã thu hút nhiều khác du lịch ưa khám phá đến với nơi đây để chiêm ngưỡng công trình vĩ đại từ 4000 năm về trước. Thực chất công trình này đã trở nên rất nổi tiếng tại thời Hy Lạp cổ đại và ngày nay nó là một kỳ quan mà cả thế giới đều phải chiêm ngưỡng.
Kim tự tháp Ai Cập được người nước ngoài xem là một nơi xa xôi ở sa mạc, mặc dù là nó nằm ở thành phố thủ đô và là nơi đông đúc và sầm uất nhất châu Phi. Cho đến bây giờ, với sự phát triển của xã hội mà kiến trúc này không còn được xem là năm ở vùng hoang vu nữa mà ngày càng có nhiều du khách đổ xô đến nơi đây để du lịch hơn.
Vì thế, du lịch châu Phi, đến với thủ đô Cairo chắc chắn sẽ không bỏ qua được công trình kim tự tháp này. Đây là công trình nhân tạo vĩ đại nhất với các khối đá được chạm khắc tinh xảo, xếp chồng lên nhau một cách hoàn hảo và vừa khít với độ cao lên đến 146,5 m.
Kim tự tháp Giza có hướng quay mặt về đúng điểm cực Bắc của trái đất và điểm đặc biệt của ba kim tự tháp là Khufu, Khafre và Menkaure nằm thẳng hàng và đúng vị trí của chòm sao thắt lưng Orion. Qua đó có thể thấy văn hóa và sự phát triển của chiêm tinh học của người Ai Cập có tính chuẩn xác cực kỳ cao.
Qua đó mà cũng có rất nhiều những giả thuyết huyền bí về kim tự tháp Giza này. Bắt nguồn từ vị vua Orion Pharaoh, được coi là vị vua Ai Cập cao quý bậc nhất. Người được xem là được thần linh lựa chọn và là trung gian để kết nối giữa con người với thần linh trên cao. Vì thế mà tên ông ấy cũng được dùng để đặt cho chòm sao Orion hiện nay.
Hiện nay, Kim tự tháp Ai Cập Giza được xem như một công trình kiến trúc cổ đại cũng như là một địa điểm du lịch lý tưởng cho những ai yêu thích những điều cổ xưa. Qua đó, mà nó xem là một tuyệt tác của người xưa để lại, là dấu tích của lịch sử, của thời gian. Mặc dù bị bào mòn bởi thời gian nhưng nó chưa bao giờ khiến du khách cũng như giới nghiên cứu khảo cổ ngừng thích thú khám phá và tìm hiểu.
Nguồn: aloviet.vn
Từ khoá: Kim tự tháp Ai Cập – Biểu tượng cổ đại của thế giới
người Ai Cập Cổ Đại xây Kim Tự Tháp (được gọi là Kim Tự Tháp Ai Cập) bằng cách nào ?
xây kim tự tháp bằng cách xây kim tự tháp
Mình đọc 7 Kỳ Quan Thế Giới rồi nhưng không nhớ (và cái đấy liên quan gì đến lịch sử lớp 4 hả bạn?)
nguyễn hà vy ơi bạn xàm quá a~ để mik trả lời cho mà nghe : để vận chuyển những khối đá lớn xây dựng kim tự tháp Giza , người Ai Cập Cổ Đại Đã biết lợi dụng sức nước , lực đẩy của nước. Ngoài việc dùng thuyền gỗ, người xưa còn sử dụng da dê và dây thừng làm thành phao nâng kéo các khối đá
kết thúc câu trả lời ... nói tóm gọn lại là như thế đó :)))
Xem thêm câu trả lời
Kim Tự Tháp ở Ai Cập là nơi để làm gì?
tham quan du lịch, khám phá bí mật bên trong,làm cảnh,...
Đúng 0
Bình luận (0)
Hình như là nơi để chứa.........,dành cho những người cực kì giàu có!
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Trong Kim tự tháp Ai Cập người ta tìm đc con số j?nêu ý nghĩa của con số đó.
Tham khảo
Được biết là dãy số “142857” được phát hiện bên trong kim tự tháp Ai Cập, điều này chứng minh rằng một tuần có 7 ngày, là sự kết hợp của bội số tăng dần, 6 chữ số này luân phiên xuất hiện một lần và nghỉ vào ngày thứ 7 để dãy số 999999 thay thế, bội số tiếp tục tăng dần, mỗi khi qua một tuần, con số cuối cùng sẽ phải ...
Đúng 1
Bình luận (2)
Kim tự tháp Cheops là kim tự tháp lớn nhất trong các kim tự tháp ở Ai Cập, được xây dựng vào thế kỉ thứ 26 trước Công nguyên và là một trong bảy kì quan của thế giới cổ đại. Kim tự tháp có dạng hình chóp với đáy là hình vuông có cạnh dài khoảng 230 m, các cạnh bên bằng nhau và dài khoảng 219 m (kích thước hiện nay). (Theo britannica.com).Tính (gần đúng) góc tạo bởi cạnh bên SC và cạnh đáy AB của kim tự tháp (H.7.4).
Đọc tiếp
Kim tự tháp Cheops là kim tự tháp lớn nhất trong các kim tự tháp ở Ai Cập, được xây dựng vào thế kỉ thứ 26 trước Công nguyên và là một trong bảy kì quan của thế giới cổ đại. Kim tự tháp có dạng hình chóp với đáy là hình vuông có cạnh dài khoảng 230 m, các cạnh bên bằng nhau và dài khoảng 219 m (kích thước hiện nay). (Theo britannica.com).
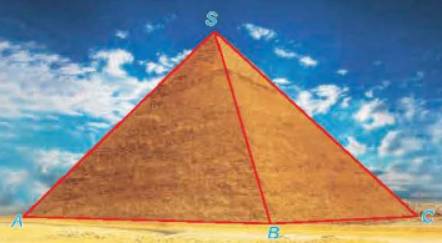
Tính (gần đúng) góc tạo bởi cạnh bên SC và cạnh đáy AB của kim tự tháp (H.7.4).
Vì AB // CD (ABCD là hình vuông) nên (SC, AB) = (SC, CD)
Xét tam giác SCD có
\(\cos \widehat {SCD} = \frac{{S{C^2} + C{D^2} - S{D^2}}}{{2SC.CD}} = \frac{{{{219}^2} + {{230}^2} - {{219}^2}}}{{2.219.230}} = \frac{{115}}{{219}} \Rightarrow \widehat {SCD} \approx 58,{32^0}\)
Vậy góc tạo bởi cạnh bên SC và cạnh đáy AB của kim tự tháp bằng khoảng 58,320.
Đúng 0
Bình luận (0)
Người Ai Cập xây Kim tự tháp để làm gì???
để là nơi yên nghỉ của vua nào ý
Đúng 0
Bình luận (0)
Kim tự tháp Kê-ôp (Kheops) ở Ai Cập có hình dạng là một hình chóp tứ giác đều. Biết chiều cao kim tự tháp là 137m, cạnh đáy dài 231m. Tính diện tích xung quanh và thể tích của kim tự tháp
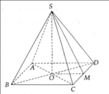
Kim tự tháp có dạng hình chóp tứ giác đều S.ABCD.
Gọi M là trung điểm của cạnh CD; O là tâm của đáy ABCD.
Tính được:
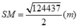
Diện tích xung quanh của kim tự tháp là:
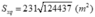
Thể tích của kim tự tháp:
V = 2436819 (m3)
Đúng 0
Bình luận (0)
Để tính cạnh bên và diện tích một mặt bên của kim tự tháp Kê-ốp, chúng ta cần sử dụng các tính chất của hình chóp tứ giác đều.
1. **Tính cạnh bên**:
Trong một hình chóp tứ giác đều, cạnh bên có thể tính được bằng cách sử dụng định lý Pythagoras trên một tam giác vuông có cạnh góc vuông là nửa đường chéo của đáy (đường chéo chia đáy thành hai phần bằng nhau), độ dài một cạnh của đáy và chiều cao của hình chóp.
Trong trường hợp này, nửa đường chéo của đáy là \( \frac{231}{2} = 115.5 \) m, chiều cao của hình chóp là 137 m. Ta sẽ tính độ dài cạnh bên như sau:
\[ \text{Cạnh bên} = \sqrt{{\text{đường chéo}^2 + \text{chiều cao}^2}} \]
\[ \text{Cạnh bên} = \sqrt{{115.5^2 + 137^2}} \]
\[ \text{Cạnh bên} ≈ \sqrt{{13340.25 + 18769}} \]
\[ \text{Cạnh bên} ≈ \sqrt{{32109.25}} \]
\[ \text{Cạnh bên} ≈ 179.25 \, \text{m} \]
2. **Tính diện tích một mặt bên**:
Diện tích một mặt bên của hình chóp tứ giác đều được tính bằng công thức:
\[ \text{Diện tích một mặt bên} = \frac{{\text{cạnh đáy} \times \text{chiều cao}}}{{2}} \]
Trong trường hợp này, cạnh đáy là 231 m và chiều cao là 137 m. Ta sẽ tính diện tích một mặt bên như sau:
\[ \text{Diện tích một mặt bên} = \frac{{231 \times 137}}{{2}} \]
\[ \text{Diện tích một mặt bên} = \frac{{31647}}{{2}} \]
\[ \text{Diện tích một mặt bên} = 15823.5 \, \text{m}^2 \]
Vậy, cạnh bên của kim tự tháp Kê-ốp là khoảng 179.25 m và diện tích của một mặt bên là khoảng 15823.5 \( \text{m}^2 \).
Đúng 0
Bình luận (0)






