Cho hai số có tích bằng 102; nếu giảm số thứ nhất đi 3 đơn vị thì tích mới bằng 84. Tìm hai số đó?
Cho hai số có tích bằng 102; nếu giảm số thứ nhất đi 3 đơn vị thì tích mới bằng 84. Tìm hai số đó?
Cho hai số có tích bằng 102; nếu tăng số thứ nhất lên 2 đơn vị thì tích mới bằng 136. Tìm hai số đó?
2 đơn vị ứng với số phần là :
136-102=34
số thứ nhất là :
34 ;2 =17
số thứ hai là
102 :107=6
vậy số thứ nhất : 17
số thứ hai 6
Gọi số thứ nhất là A , số thứ hai là B
A x B = 102
( A +2) x B = 136
A x B + 2 x B = 136
102 + B x 2 = 136
B x 2 = 136 - 102
B x 2 = 34
B = 34:2= 17
A = 102 : 17 = 6
Cho 2 số có tích bằng 102. Nếu tăng số thứ nhất lêm 2 đơn vị thì tích mới bằng 136. Tìm hai số đó
goi 2 so do la a va b
axb=102
(a+2)xb=136
axb+2b=136
102+2b=136
2b=136-102
2b=34
b=34:2
b=17
a=102:17
a=6
vay so thu nhat la 6,thu 2 la 17
số thứ nhất là 6
số thứ hai là 17
đúng ko ?
1) Một số khi chia cho 98 dư 82. Hỏi số đó chia cho 14 dư mấy?
2) Cho 2 số có tích bằng 102. Nếu tăng số thứ nhất lêm 2 đơn vị thì tích mới bằng 136. Tìm hai số đó
Gọi số đó là 98k+82
Ta có:98k+82
=(98k+70)+12
=14(7k+5)+12
Do 14(7k+5) chia hết cho 14
=>14(7k+5) + 12 chia 14 dư 12
=>số chia 98 dư 82 thì chia 14 dư 12
Gọi số đó là 98k+82
Ta có:98k+82
=(98k+70)+12
=14(7k+5)+12
Do 14(7k+5) chia hết cho 14
=>14(7k+5) + 12 chia 14 dư 12
=>số chia 98 dư 82 thì chia 14 dư 12
Mình chắc chắn là đúng
1. Tìm hai số nguyên tố có tổng là 1055.
2. Tìm ba số tự nhiên lẻ liên tiếp có tích bằng 12075.
3. Tìm hai số tự nhiên x và y biết:
( x + 5 ) . ( y + 2 ) = 102
bài 3
( x + 5 ) . ( y + 2 ) = 102
ta có :\(y+2\inƯ\left(102\right)\)
mà \(y+2\ge2\)
nên \(y+2=2\)hoặc \(y+2=3\)
TH1 nếu \(y+2=2\)
=>\(y=1\)
Do \(y+2=2\)nên \(x+5=51\)
=>\(x=46\)
TH2 nếu \(y+2=3\)
=>\(y=1\)
Do \(y+2=3\)nên \(x+5=34\)
=>\(x=29\)
Vậy cặp số x;y lần lượt là :
nếu y=0 thì x=46
nếu y=1 thì x=29
a) x4+x3+2x2+x+1=(x4+x3+x2)+(x2+x+1)=x2(x2+x+1)+(x2+x+1)=(x2+x+1)(x2+1)
b)a3+b3+c3-3abc=a3+3ab(a+b)+b3+c3 -(3ab(a+b)+3abc)=(a+b)3+c3-3ab(a+b+c)
=(a+b+c)((a+b)2-(a+b)c+c2)-3ab(a+b+c)=(a+b+c)(a2+2ab+b2-ac-ab+c2-3ab)=(a+b+c)(a2+b2+c2-ab-ac-bc)
c)Đặt x-y=a;y-z=b;z-x=c
a+b+c=x-y-z+z-x=o
đưa về như bài b
d)nhóm 2 hạng tử đầu lại và 2hangj tử sau lại để 2 hạng tử sau ở trong ngoặc sau đó áp dụng hằng đẳng thức dề tính sau đó dặt nhân tử chung
e)x2(y-z)+y2(z-x)+z2(x-y)=x2(y-z)-y2((y-z)+(x-y))+z2(x-y)
=x2(y-z)-y2(y-z)-y2(x-y)+z2(x-y)=(y-z)(x2-y2)-(x-y)(y2-z2)=(y-z)(x2-2y2+xy+xz+yz)
Tích của hai số tự nhiên a và b bằng 102, hiệu hai số là a − b = 49. Tìm hai số a, b.
Thách ai giải được bài này
tập hợp rỗng vì không có hiệu nào là a-b=49 mà tích lại bằng 102
câu hỏi hơi tấu nhưng gặp ...🤣🤣🤣🤣🤣🤣
a. Tích của hai số a; b bằng 42. Biết a < b, tìm hai số a và b
b. Tìm các số tự nhiên x; y biết x + 5 y + 2 = 102
a, Tích của hai số a; b bằng 42. Biết a < b, tìm hai số a và b
b, Tìm các số tự nhiên x; y biết (x+5)(y+2) = 102
a, Ta có: 42 = 2.3.7 = 1.42 = 2.21 = 3.14 = 6.7
Vì a < b nên ta tìm được các cặp số (a ;b) là (1;42), (2;21), (3;14), (6;7)
b, Ta có: 102 = 2.3.17 = 2.51 = 3.34 = 6.17
Vì x; y là số tự nhiên nên x + 5 ≥5 ; y + 2 ≥ 2. Khi đó (x+5)(y+2) = 51.2 = 34.3 = 6.17 = 17.6
Ta có bảng sau:
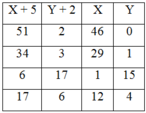
Vậy có các cặp nghiệm (x;y) thỏa mãn đề bài là: (46;0), (29;1), (1;15), (12;4)
1. Tìm hai số nguyên tố có tổng là 1055.
2. Tìm ba số tự nhiên lẻ liên tiếp có tích bằng 12075.
3. Tìm hau số tự nhiên x và y biết:
( x + 5 ) . ( y + 2 ) = 102