mẫu số trung của 35,180,28
TH
Những câu hỏi liên quan
BCNN(35,180,28)=?
\(35=5.7\\ 180=2^2.3^2.5\\ 28=2^2.7\\ \Rightarrow BCNN\left(35,180,28\right)=2^2.3^2.5.7=1260\)
Đúng 3
Bình luận (0)
Xem thêm câu trả lời
Cho mẫu số liệu: 1 2 4 5 9 10 11a) Số trung bình cộng của mẫu số liệu trên là:A. 5. B. 5,5. C.6. D. 6,5.b) Trung vị của mẫu số liệu trên là:A. 5. B. 5,5. C. 6. D. 6,5.c) Tứ phân vị của mẫu số liệu trên là:A.{Q_1}{rm{ }} {rm{ }}4,{rm{ }}{Q_2}{rm{ }} {rm{ }}5,{rm{ }}{Q_3}{rm{ }} {rm{ }}9 .B.{Q_1}{rm{ }} {rm{ }}1,{rm{ }}{Q_2}{rm{ }} {rm{ }}5,5,{rm{ }}{Q_3}{rm{ }} {rm{ }}11 .C.{Q_1}{rm{ }}...
Đọc tiếp
Cho mẫu số liệu: 1 2 4 5 9 10 11
a) Số trung bình cộng của mẫu số liệu trên là:
A. 5. B. 5,5. C.6. D. 6,5.
b) Trung vị của mẫu số liệu trên là:
A. 5. B. 5,5. C. 6. D. 6,5.
c) Tứ phân vị của mẫu số liệu trên là:
A.\({Q_1}{\rm{ }} = {\rm{ }}4,{\rm{ }}{Q_2}{\rm{ }} = {\rm{ }}5,{\rm{ }}{Q_3}{\rm{ }} = {\rm{ }}9\) .
B.\({Q_1}{\rm{ }} = {\rm{ }}1,{\rm{ }}{Q_2}{\rm{ }} = {\rm{ }}5,5,{\rm{ }}{Q_3}{\rm{ }} = {\rm{ }}11\) .
C.\({Q_1}{\rm{ }} = {\rm{ }}1,{\rm{ }}{Q_2}{\rm{ }} = {\rm{ }}5,{\rm{ }}{Q_3}{\rm{ }} = {\rm{ }}11\) .
D.\({Q_1}{\rm{ }} = {\rm{ }}2,{\rm{ }}{Q_2}{\rm{ }} = {\rm{ }}5,{Q_3} = {\rm{ }}10\) .
d) Khoảng biến thiên của mẫu số liệu trên là:
A. 5. B. 6. C. 10. D. 11.
e) Khoảng tứ phân vị của mẫu số liệu trên là:
A. 7. B. 8. C. 9. D. 10.
g) Phương sai của mẫu số liệu trên là:
A.\(\sqrt {\frac{{96}}{7}} \) B.\(\frac{{96}}{7}\) C. 96. D.\(\sqrt {96} \) .
h) Độ lệch chuẩn của mẫu số liệu trên là:
A.\(\sqrt {\frac{{96}}{7}} \) B.\(\frac{{96}}{7}\) C. 96. D.\(\sqrt {96} \) .
*) Sắp xếp thứ tự của mẫu số liệu theo thứ tự không giảm ta được: 1 2 4 5 9 10 11
a) Số trung bình cộng của mẫu số liệu trên là: \(\overline x = \frac{{1{\rm{ + }}2{\rm{ + }}4{\rm{ + }}5{\rm{ + }}9{\rm{ + }}10{\rm{ + }}11}}{7} = 6\)
b) Trung vị của mẫu số liệu trên là: Do mẫu số liệu trên có 7 số liệu ( lẻ ) nên trung vị \({Q_2} = 5\)
c) Tứ phân vị của mẫu số liệu trên là:
Trung vị của dãy 1, 2, 4 là: \({Q_1} = 2\)
Trung vị của dãy 9, 10, 11 là: \({Q_3} = 10\)
Vậy tứ phân vị của mẫu số liệu là: \({Q_1} = 2\), \({Q_2} = 5\), \({Q_3} = 10\)
d) Khoảng biến thiên của mẫu số liệu trên là: \(R = {x_{\max }} - {x_{\min }} = 11 - 1 = 10\)
e) Khoảng tứ phân vị của mẫu số liệu trên là: \({\Delta _Q} = {Q_3} - {Q_1} = 10 - 2 = 8\)
g) Phương sai của mẫu số liệu trên là: \({s^2} = \frac{{\left[ {{{\left( {1 - \overline x } \right)}^2} + {{\left( {2 - \overline x } \right)}^2} + ... + {{\left( {11 - \overline x } \right)}^2}} \right]}}{7} = \frac{{96}}{7}\)
h) Độ lệch chuẩn của mẫu số liệu trên là: \(s = \sqrt {{s^2}} = \sqrt {\frac{{96}}{7}} \)
Đúng 0
Bình luận (0)
Cho mẫu số liệu gồm bốn số tự nhiên khác nhau và khác 0, biết số trung bình là 6 và số trung vị là 5. Tìm các giá trị của mẫu số liệu đó sao cho hiệu của giá trị lớn nhất và giá trị nhỏ nhất của mẫu số liệu đạt giá trị nhỏ nhất. A. 3;4;6;11 B. 2;4;7;11 C. 3;5;6;11 D. 2;4;6;12
Đọc tiếp
Cho mẫu số liệu gồm bốn số tự nhiên khác nhau và khác 0, biết số trung bình là 6 và số trung vị là 5. Tìm các giá trị của mẫu số liệu đó sao cho hiệu của giá trị lớn nhất và giá trị nhỏ nhất của mẫu số liệu đạt giá trị nhỏ nhất.
A. 3;4;6;11
B. 2;4;7;11
C. 3;5;6;11
D. 2;4;6;12
Chọn A.
Giả sử các giá trị của mẫu số liệu là a; b; c; d với 0 < a < b < c < d và a; b; c;d là số tự nhiên.
+ Ta có 
Mà số trung bình là 6 nên a + b + c + d = 24
Suy ra a + d = 14
+ Ta có 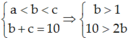 hay 1 < b < 5 mà b là số tự nhiên nên b = 2; 3; 4
hay 1 < b < 5 mà b là số tự nhiên nên b = 2; 3; 4
+ Nếu b = 2 thì c = 8, mà 0 < a < b; a là số tự nhiên nên a = 1 và d = 13
Khi đó các giá trị của mẫu số liệu là 1; 2; 8; 13
+ Nếu b = 3 thì c = 7, mà 0 < a < b; a số tự nhiên nên có 2 khả năng xảy ra: a = 1 ; d = 13 hoặc a = 2 ; d = 12
Khi đó có hai mẫu số liệu thỏa đề bài có giá trị là 1;3;7;13 và 2;3;7;12
+ Nếu b = 4 thì c = 6, mà 0 < a < b; a là số tự nhiên nên có 3 khả năng xảy ra:
a = 1; d = 13 hoặc a = 2 ; d = 12 hoặc a = 3 ; d = 11
Khi đó có ba mẫu số liệu thỏa đề bài có giá trị là 1;4;6;13 hoặc 2;4;6;12 hoặc 3;4;6;11
Suy ra với mẫu số liệu có các giá trị là 3;4;6;11 thì hiệu của giá trị lớn nhất và giá trị nhỏ nhất của mẫu số liệu đạt giá trị nhỏ nhất.
Đúng 0
Bình luận (1)
Cho mẫu số liệu thống kê {6;4;4;1;9;10;7} . Số liệu trung vị của mẫu số liệu thống kê trên là:
A. 1
B. 6
C. 4
D. 10
Đáp án B.
Sắp thứ tự các số liệu thống kê thành một dãy không giảm là:
1 4 4 6 7 9 10
Vậy số trung vị là M e = 6
Chú ý: Cách tìm số trung vị M e = 6
+ Sắp thứ tự các số liệu thống kê thành 1 dãy không giảm (không tăng).
+ Nếu số phần tử lẻ thì M e = 6 là số đứng giữa dãy.
+ Nếu số phần tử chẵn thì M e = 6 là trung bình cộng của 2 số đứng giữa dãy.
Đúng 1
Bình luận (0)
Trung bình cộng của tử số và mẫu số của một phân số là 5. Mẫu số lớn hơn tử số 4 đơn vị. Tìm phân số đó.
tổng của tử và mẫu là:5*2=10 mẪU SỐ LÀ:(10+4):2=7 TỬ SỐ LÀ:10-7=3 PS ĐÓ LÀ :3/7
Đúng 2
Bình luận (0)
TỔNG CỦA TỬ VÀ MẪU:
5x2=10
MẪU SỐ LÀ:
(10+4):2=7
TỬ SỐ LÀ:10-7=3
PS ĐÓ LÀ :3/7
Đúng 1
Bình luận (0)
Dùng các mẫu đất đã chuẩn bị từ nhà và làm theo các bước đã được trình bài ở trên. Mỗi mẫu đất làm 3 lần và lấy kết quả trung bình. Ghi kết quả thu được vào vở bài tập theo mẫu bảng sau:
Mẫu đất
Độ pH
Đất chua, kiềm, trung tính
Mẫu số 1. So lần 1
Mẫu số 1. So lần 2
Mẫu số 1. So lần 3
Mẫu số 1. Trung bình
Mẫu số 2. So lần 1
Mẫu số 2....
Đọc tiếp
Dùng các mẫu đất đã chuẩn bị từ nhà và làm theo các bước đã được trình bài ở trên. Mỗi mẫu đất làm 3 lần và lấy kết quả trung bình. Ghi kết quả thu được vào vở bài tập theo mẫu bảng sau:
| Mẫu đất | Độ pH | Đất chua, kiềm, trung tính |
| Mẫu số 1. So lần 1 | ||
| Mẫu số 1. So lần 2 | ||
| Mẫu số 1. So lần 3 | ||
| Mẫu số 1. Trung bình | ||
| Mẫu số 2. So lần 1 | ||
| Mẫu số 2. So lần 2 | ||
| Mẫu số 2. So lần 3 | ||
| Mẫu số 2. Trung bình |
| Mẫu đất | Độ pH | Đất chua, kiềm, trung tính |
| Mẫu số 1. So lần 1 | 4.0 | Đất chua |
| Mẫu số 1. So lần 2 | 4.0 | Đất chua |
| Mẫu số 1. So lần 3 | 4.5 | Đất chua |
| Mẫu số 1. Trung bình | 4.167 | Đất chua |
| Mẫu số 2. So lần 1 | 5.0 | Đất chua |
| Mẫu số 2. So lần 2 | 5.5 | Đất chua |
| Mẫu số 2. So lần 3 | 4.0 | Đất chua |
| Mẫu số 2. Trung bình | 4.83 | Đất chua |
Đúng 0
Bình luận (0)
Tìm 1 phân số trung bình cộng của tử số và mẫu số là 16, mẫu số hơn tử số 6 đơn vị
Xem chi tiết
2/8 hoặc là 2/6 mk cũng ko rõ nx
\(\frac{11}{5}\)
tổng của tử va mẫu là
16*2=32
mẫu là
(32+6)/2=19
tử là 32-19=13
vậy phân số đó là 13/19
Tìm một phân số biết trung bình cộng của tử số và mẫu số là 12;tử số hơn mẫu số 6 đơn vị.
Xem chi tiết
Tổng của tử và mẫu là:
12 x 2 = 24
Tử số là:
(24 + 6) : 2 = 15
Mẫu số là:
24 - 15 = 9
Phân số đó là: \(\frac{9}{15}\)
Tìm 1 phân số bé hơn 1 có trung bình cộng của tử số và mẫu số là 55. Hiệu của tử số và mẫu số là 28
Vì khi cộng tử với 28 ta được phân số mới bằng 1 => hiệu giữa mẫu với tử là 28.
Tổng của tử và mẫu là: 55.2=110
Tử số của phân số cần tìm là: (110-28):2=41
Mẫu số của phân số cần tìm là: 41+28=69
Vậy phân số cần tìm là: 41/69.
Giải
Tổng của tử số và mẫu số là: 55 x 2 = 110
Tử số là: (110 - 28) : 2 = 41
Mẫu số là: 110 - 41 = 69
Vậy phân số cần tìm là: \(\frac{41}{69}\)
Đáp số: \(\frac{41}{69}\)
Chúc bạn học tốt :33
bn ươiiiiiiiiiiiiiiiii
nhớ tíc cho toi nha
mất công lm cho bn phải rủ lòng hương k cho toi
T_T
Xem thêm câu trả lời




