Cho mặt cầu (S):x^2+y^2+z^2+x-2y+4z-3=0.Xác định tọa độ tâm I của mặt cầu.
BN
Những câu hỏi liên quan
Trong không gian Oxyz, cho mặt cầu (S):
(
x
+
3
)
2
+
(
y
+
1
)
2
+
(
z
-
1
)
2
2
. Xác định tọa độ tâm của mặt cầu A. I(-3;1;-1) B. I(3;1;-1) C. I(-3;-1;1) D. I(3;-1;1)
Đọc tiếp
Trong không gian Oxyz, cho mặt cầu (S): ( x + 3 ) 2 + ( y + 1 ) 2 + ( z - 1 ) 2 = 2 . Xác định tọa độ tâm của mặt cầu
A. I(-3;1;-1)
B. I(3;1;-1)
C. I(-3;-1;1)
D. I(3;-1;1)
Cho mặt phẳng left(Pright):2x-3y+4z-50 và mặt cầu left(Sright):x^2+y^2+z^2+3x+4y-5z+60
a) Xác định tọa độ tâm I và bán kính r của mặt cầu (S)
b) Tính khoảng cách từ tâm I đến mặt phẳng (P). Từ đó chứng minh rằng mặt phẳng (P) cắt mặt cầu (S) theo một đường tròn mà ta kí hiệu là (C). Xác định bán kính r và tâm H của đường tròn (C)
Đọc tiếp
Cho mặt phẳng \(\left(P\right):2x-3y+4z-5=0\) và mặt cầu \(\left(S\right):x^2+y^2+z^2+3x+4y-5z+6=0\)
a) Xác định tọa độ tâm I và bán kính r của mặt cầu (S)
b) Tính khoảng cách từ tâm I đến mặt phẳng (P). Từ đó chứng minh rằng mặt phẳng (P) cắt mặt cầu (S) theo một đường tròn mà ta kí hiệu là (C). Xác định bán kính r' và tâm H của đường tròn (C)
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) : x²+y²+z²-2x+4z+10. Tâm của mặt cầu là điểm: A. I(1;-2;0) B. I(1;0;-2) C. I(-1;2;0) D. I(0;1;2).
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) : x²+y²+z²-2x+4z+1=0. Tâm của mặt cầu là điểm:
A. I(1;-2;0)
B. I(1;0;-2)
C. I(-1;2;0)
D. I(0;1;2).
Đáp án B
Ta có (S): (x-1)²+y²+(z+2)²=4 => (S) có tâm I(1;0;-2).
Đúng 0
Bình luận (0)
Cho mặt cầu(S) có phương trình
x
-
3
2
+
y
+
2
2
+
z
-
1
2
100
và mặt phẳng (α) có phương trình 2x – 2y – z + 9 0. Mp(α) cắt mặt cầu (S) theo m...
Đọc tiếp
Cho mặt cầu(S) có phương trình x - 3 2 + y + 2 2 + z - 1 2 = 100 và mặt phẳng (α) có phương trình 2x – 2y – z + 9 = 0. Mp(α) cắt mặt cầu (S) theo một đường tròn (C). Hãy xác định tọa độ tâm và tính bán kính của đường tròn (C).
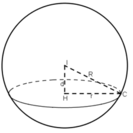
Từ phương trình x - 3 2 + y + 2 2 + z - 1 2 = 100 ta suy ra mặt cầu (S) có tâm I(3;-2;1) và có bán kính R=10. Gọi H là tâm cả đường tròn (C) - Hình chiếu vuông góc của I trên mặt phẳng ( α )
Phương trình tham số của đường thẳng IH là:
x
=
3
+
2
t
y
=
-
2
-
2
t
z
=
1
-
t
Thay x,y,z từ phương trình tham số của đường thẳng IH vào phương trình mp
α
tại H(-1;2;3). H là tâm của đường tròn (C). Vậy bán kính của đường tròn (C) là ![]()
Đúng 0
Bình luận (0)
Trong không gian Oxyz , cho mặt cầu
S
:
x
+
3
3
+
y
+
1
2
+
z
-
1
2
2
. Xác định tọa độ tâm của mặt cầu...
Đọc tiếp
Trong không gian Oxyz , cho mặt cầu S : x + 3 3 + y + 1 2 + z - 1 2 = 2 . Xác định tọa độ tâm của mặt cầu s .
A. I - 3 , 1 , - 1
B. I 3 , 1 , - 1
C. I - 3 , - 1 , 1
D. I 3 , - 1 , 1
Mặt cầu
![]()
có tâm . I - 3 , - 1 , 1
Chọn: C
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S): x²+y²+z²-x+2y+10. Tìm tọa độ tâm I và bán kính R của (S). A. I(-1/2;1;0) và R 1/4 B. I(1/2;1;0) và R 1/2 C. I(1/2;-1;0) và R 1/2 D. I(-1/2;1;0) và R 1/2
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S): x²+y²+z²-x+2y+1=0. Tìm tọa độ tâm I và bán kính R của (S).
A. I(-1/2;1;0) và R = 1/4
B. I(1/2;1;0) và R = 1/2
C. I(1/2;-1;0) và R = 1/2
D. I(-1/2;1;0) và R = 1/2
Đáp án C
Theo công thức tính tâm và bán kính mặt cầu từ phương trình tổng quát, với a = - 1/2, b = 1, c = 0 và d=1 ta có tâm I(1/2;-1;0) và R = 1/2
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng
(
P
)
:
2
x
−
2
y
−
z
−
9
0
và mặt cầu
(
S
)
:
(
x
−
3
)
2
+
(
y
+
2...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng ( P ) : 2 x − 2 y − z − 9 = 0 và mặt cầu ( S ) : ( x − 3 ) 2 + ( y + 2 ) 2 + ( z − 1 ) 2 = 100 . Biết (P) cắt (S) theo giao tuyến là một đường tròn. Tìm tọa độ tâm của đường tròn giao tuyến.
A. (3;2;-1)
B. (-3;2;-1)
C. (3;-2;1)
D. (-3;2;1)
Trong không gian hệ tọa độ Oxyz, cho mặt cầu (S):
(
x
-
1
)
2
+
(
y
+
2
)
2
+
(
z
-
3
)
2
4
. Tìm tọa độ tâm I và bán kính R của mặt cầu đó A. I(-1;2;3), R2 B. I(-1;2;-3), R...
Đọc tiếp
Trong không gian hệ tọa độ Oxyz, cho mặt cầu (S): ( x - 1 ) 2 + ( y + 2 ) 2 + ( z - 3 ) 2 = 4 . Tìm tọa độ tâm I và bán kính R của mặt cầu đó
A. I(-1;2;3), R=2
B. I(-1;2;-3), R=4
C. I(1;-2;3); R=2
D. I(1;-2;3), R=4
Trong hệ tọa độ Oxyz, cho mặt cầu (S) có phương trình : left(x-3right)^2+left(y+2right)^2+left(z-1right)^2100 và mặt phẳng left(alpharight) có phương trình 2x-2y-z+90. Mặt phẳng left(alpharight) cắt mặt cầu (S) theo một đường tròn (C)
Hãy xác định tọa độ tâm và tính bán kính của đường tròn (C) ?
Đọc tiếp
Trong hệ tọa độ Oxyz, cho mặt cầu (S) có phương trình : \(\left(x-3\right)^2+\left(y+2\right)^2+\left(z-1\right)^2=100\) và mặt phẳng \(\left(\alpha\right)\) có phương trình \(2x-2y-z+9=0\). Mặt phẳng \(\left(\alpha\right)\) cắt mặt cầu (S) theo một đường tròn (C)
Hãy xác định tọa độ tâm và tính bán kính của đường tròn (C) ?

Mặt cầu (S) có tâm I(3, -2, 1) và bán kính R = 10.
Khoảng cách từ tâm I của mặt cầu (S) đến mặt phẳng (α) là:
d(I, α) = ∣∣ ∣∣2.3−2.(−2)−1+9√22+(−2)2+(−1)2∣∣ ∣∣=183=6|2.3−2.(−2)−1+922+(−2)2+(−1)2|=183=6
Vì d(I, α) < R ⇒⇒ Mặt phẳng (α) cắt mặt cầu (S) theo đường tròn (C) có phương trình (C):
{2x−2y−z+9=0(x−3)2+(y+2)2+(z−1)2=100{2x−2y−z+9=0(x−3)2+(y+2)2+(z−1)2=100
Tâm K của đường tròn (C) là hình chiếu vuông góc của tâm I của mặt cầu trên mặt phẳng (α).
Mặt phẳng (α) có vectơ pháp tuyến →nn→ = (2, -2. -1).
Đường thẳng d qua I và vuông góc với (α) nhận →nn→ = (2, -2, -1) làm vectơ chỉ phương và có phương trình d :
⎧⎪⎨⎪⎩x=3+2ty=−2−2tz=1−t{x=3+2ty=−2−2tz=1−t
Thay t = -2 vào phương trình của d, ta được toạ độ tâm K của đường tròn (C).
⎧⎪⎨⎪⎩x=3+2.(−2)=−1y=−2−2.(−2)=2z=1−2.(−2)=3{x=3+2.(−2)=−1y=−2−2.(−2)=2z=1−2.(−2)=3
⇒⇒ K(-1, 2, 3)
Ta có: IK2 = (-1 - 3)2 + (2 + 2)2 + (3 - 1)2 = 36.
Bán kính r của đường tròn (C) là:
r2 = R2 - IK2 = 102 - 36 = 64 ⇒⇒ r= 8
Đúng 0
Bình luận (0)
Giải

Mặt cầu (S) có tâm I(3, -2, 1) và bán kính R = 10.
Khoảng cách từ tâm I của mặt cầu (S) đến mặt phẳng (α) là:
d(I, α) = ∣∣ ∣∣2.3−2.(−2)−1+9√22+(−2)2+(−1)2∣∣ ∣∣=183=6|2.3−2.(−2)−1+922+(−2)2+(−1)2|=183=6
Vì d(I, α) < R ⇒⇒ Mặt phẳng (α) cắt mặt cầu (S) theo đường tròn (C) có phương trình (C):
{2x−2y−z+9=0(x−3)2+(y+2)2+(z−1)2=100{2x−2y−z+9=0(x−3)2+(y+2)2+(z−1)2=100
Tâm K của đường tròn (C) là hình chiếu vuông góc của tâm I của mặt cầu trên mặt phẳng (α).
Mặt phẳng (α) có vectơ pháp tuyến →nn→ = (2, -2. -1).
Đường thẳng d qua I và vuông góc với (α) nhận →nn→ = (2, -2, -1) làm vectơ chỉ phương và có phương trình d :
⎧⎪⎨⎪⎩x=3+2ty=−2−2tz=1−t{x=3+2ty=−2−2tz=1−t
Thay t = -2 vào phương trình của d, ta được toạ độ tâm K của đường tròn (C).
⎧⎪⎨⎪⎩x=3+2.(−2)=−1y=−2−2.(−2)=2z=1−2.(−2)=3{x=3+2.(−2)=−1y=−2−2.(−2)=2z=1−2.(−2)=3
⇒⇒ K(-1, 2, 3)
Ta có: IK2 = (-1 - 3)2 + (2 + 2)2 + (3 - 1)2 = 36.
Bán kính r của đường tròn (C) là:
r2 = R2 - IK2 = 102 - 36 = 64 ⇒⇒ r= 8
Đúng 0
Bình luận (0)








