1 khẳng định:Tồn tại tam giác có độ dài ba cạnh a,b,c sao cho a=2b;b=2c là đúng hay sai?
2 Tìm số nguyên dương a lớn nhất sao cho 2004! chia hết cho 7a
3 Tìm các số nguyên tố x,y sao cho 51x+26y=2000
Khẳng định:'' Tồn tại tam giác có độ dài 3 cạnh là a,b,c sao cho a=2b, b=2c'' là đúng hay sai?
Sai vì:
a = 2b; b = 2c nên a = 4c
ta xét:a và b + c
a = 4c
b + c = 2c + c = 3c
4c > 3c nên a > b + c (Trái với Định lý BĐT trong tam giác)
Vậy không tồn tại tam giác có độ dài 3 cạnh là a; b; c sao cho a = 2b; b = 2c
Tích mình đi, mình tích lại cho
a=2b;b=3c
Suy ra:a=2b=4c
b =2c
c =1c
áp dụng định lý pi-ta-go
Suy ra:42=12+22
Mà 42 không bằng 12+22
vậy ta có thể khẳng định không tồn tại tam giác có độ dài ba cạnh là a;b;c sao cho a=2b;b=2c
a=2b;b=2c
a=2b=4c
b=2c
c=1c
mà a(4c)>b+c(2+1) hay 4c>2c+1c
Áp dụng bất đẳng thức trong tam giác''tổng hai cạnh bất kì bao giờ cŨNG lớn hơn cạnh còn lại
Vậy khẳng định này là sai
Khẳng định " tồn tại tam giác có độ dài 3 cạnh là a ; b ; c sao cho a=2b , b=2c " là đúng hay sai ( gải thích tại sao nha ) m.n giúp mk với akaka
Tồn tại hay không một tam giác có độ dài 3 cạnh là a;b;c sao cho a=2b;b=2c
cho tam giác ABC có độ dài ba cạnh là a,b,c sao cho (a+2b)/5 = (b+2c)/7 = (c+2a)/9. Tìm tỉ lệ của ba đường cao tương ứng
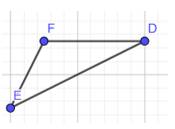
a) Cho tam giác DEF có góc F là góc tù. Cạnh nào là cạnh có độ dài lớn nhất trong ba cạnh của tam giác DEF?
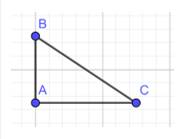
b) Cho tam giác ABC vuông tại A. Cạnh nào là cạnh có độ dài lớn nhất trong ba cạnh của tam giác ABC?
a) Vì tổng số đo 3 góc trong tam giác là 180° mà F là góc tù
\( \Rightarrow \) F > 90° do F là góc tù
\( \Rightarrow \) D + E < 180° - 90°
\( \Rightarrow \) F là góc lớn nhất trong tam giác DEF
\( \Rightarrow \) Cạnh đối diện góc F sẽ là cạnh lớn nhất tam giác DEF
\( \Rightarrow \) DE là cạnh lớn nhất
b) Tam giác ABC có góc A là góc vuông nên ta có
\( \Rightarrow \widehat B + \widehat C = {90^o} \Rightarrow \widehat B;\widehat C < {90^o}\)
\( \Rightarrow \)A là góc lớn nhất tam giác ABC
\( \Rightarrow \)BC là cạnh lớn nhất tam giác ABC do đối diện góc A
Cho ABC có B B = 60 , A = 2 cm,BC = 5 cm. Trên cạnh BC lấy điểm D sao cho
BA BD = .
a) Chứng minh tam giác ABD đều;
b) Gọi H là trung điểm của BD. Chứng minh AH BD ⊥ ;
c) Tính độ dài cạnh AC;
d) Tam giác ABC có là tam giác vuông không? Tại sao?
cho tam giác a,b,c có đọ dài là ba cạnh của 1 tam giác C/M A= 4a^2b^2-(a^2+b^2-c^2) > 0
BẤT ĐẲNG THỨC TAM GIÁC (LỚP 7)
1. Cho đoạn thẳng có độ dài a, b. Biết rằng với tam giác có 3 cạnh là a + 5b, 5a + 6b, 3a +2b. Hỏi 2 số a, b số nào lớn hơn?
2. Cho 2 cạnh của 1 tam giác lần lượt có độ dài a, b. Hỏi chu vi của nó có thể lấy giá trị trong khoảng nào?
3. CM: Độ dài đường trung tuyến AM của tam giác ABC thỏa mãn AM < 1/2(AB + AC)
4. Cho a, b, c là các độ dài 3 cạnh của 1 tam giác. CM: Có các số dương x, y, z sao cho a = x + y, b = y + z, c = x + z.
cho a,b,c là độ dài ba cạnh của 1 tam giác
C/M A=4a^2b^2-(a^2+b^2-c^2)^2>0
Từ giả thiết suy ra
(a-b)^2+(b-c)^2+(a-c)^2=0 (nhân bung cái này sẽ ra cái giả thiết ban đầu).
Từ đó suy ra: a=b, b=c và c=a. (Do tổng của 3 bình phương mà lại bằng 0 tức là các bình phương đó đều phải bằng 0). Suy ra tam giác đó đều
P/s: Tham khảo nhé
\(A=4a^2b^2-\left(a^2+b^2-c^2\right)^2=\left(2ab\right)^2-\left(a^2+b^2-c^2\right)^2\)
\(=\left(2ab-a^2-b^2+c^2\right)\left(2ab+a^2+b^2-c^2\right)\)
\(=\left[c^2-\left(a-b\right)^2\right]\left[\left(a+b\right)^2-c^2\right]\)
\(=\left(c-a+b\right)\left(c+a-b\right)\left(a+b+c\right)\left(a+b-c\right)\)
Do a;b;c là độ dài 3 cạnh tam giác nên \(c>a-b;c>b-a;a+b+c>0;a+b>c\)
\(\Rightarrow c-a+b>0;c+a-b>0;a+b+c>0;a+b-c>0\)
Nên \(\left(c-a+b\right)\left(c+a-b\right)\left(a+b+c\right)\left(a+b-c\right)>0\)
Hay \(A>0\)(đpcm)