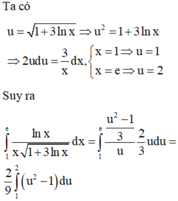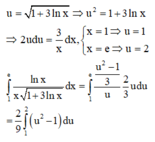CÁCH trở thành 1 IT
NV
Những câu hỏi liên quan
Cho 3 điện trở R1=10Ω. Hỏi có mấy cách mắc 3 điện trở thành 1 mạch điện ? Vẽ sơ đồ mạch điện rồi tính điện trở tương đương
(lấy 3 đtrở R1 là R1=R2=R3=10(ôm)
cách 1: R1 nt R2 nt R3=>Rtd=R1+R2+R3=30(ôm)
casch2: R1//R2//R3\(=>\dfrac{1}{Rtd}=\dfrac{1}{R1}+\dfrac{1}{R2}+\dfrac{1}{R3}=>Rtd=3,33\left(om\right)\)
cách 3 R1 nt (R2//R3)
\(=>Rtd=R1+\dfrac{R2R3}{R2+R3}=15\left(om\right)\)
cách 4: (R1 nt R2)//R3
\(=>Rtd=\dfrac{R3\left(R1+R2\right)}{R1+R2+R3}=\dfrac{20}{3}\left(om\right)\)
Đúng 4
Bình luận (0)
Với cách biến đổi
u
1
+
3
ln
x
thì tích phân
∫
1
e
ln
x
x
1
+
3
ln
x
d
x
trở thành A.
2...
Đọc tiếp
Với cách biến đổi u = 1 + 3 ln x thì tích phân ∫ 1 e ln x x 1 + 3 ln x d x trở thành
A. 2 3 ∫ 1 2 u 2 − 1 d u
B. 2 9 ∫ 1 2 u 2 − 1 d u
C. 2 ∫ 1 2 u 2 − 1 d u
D. 9 2 ∫ 1 2 u 2 − 1 u d u
1, Có 4 điện trở R1 10 R2 10 ; R3 30 R4 40a, Dùng 3 điện trở R1 ; R2 ; R3 có thể mắc thành bao nhiêu mạch điện khác nhau?.Tính điện trở tương đương của mỗi mạch điện đó. b, Hãy tìm cách mắc cả 4 điện trở thành mạch điện có điện trở 16 ôm. Vẽ sơ đồ cách mắc đó.
Đọc tiếp
1, Có 4 điện trở R1 = 10 R2 = 10 ; R3 = 30 R4 = 40
a, Dùng 3 điện trở R1 ; R2 ; R3 có thể mắc thành bao nhiêu mạch điện khác nhau?.Tính điện trở tương đương của mỗi mạch điện đó.
b, Hãy tìm cách mắc cả 4 điện trở thành mạch điện có điện trở 16 ôm. Vẽ sơ đồ cách mắc đó.
a) Để tính số mạch điện khác nhau có thể mắc từ 3 điện trở R1, R2, R3, ta sử dụng công thức tính số cách kết hợp chập k của n phần tử. Trong trường hợp này, chúng ta có n = 3 và k = 3.
Số mạch điện khác nhau = C(3, 3) = 1
Vậy có 1 mạch điện khác nhau có thể mắc từ 3 điện trở R1, R2, R3.
Điện trở tương đương của mạch điện này là R1 + R2 + R3 = 10 + 10 + 30 = 50 Ω.
b) Để mắc cả 4 điện trở thành mạch điện có điện trở 16 Ω, chúng ta có thể sử dụng mạch nối tiếp và song song.
Cách mắc như sau:
Đặt R1 và R2 nối tiếp nhau: R12 = R1 + R2 = 10 + 10 = 20 ΩR3 nối song song với R12: R123 = 1/(1/R12 + 1/R3) = 1/(1/20 + 1/30) = 12 ΩR4 nối tiếp với R123: R1234 = R123 + R4 = 12 + 40 = 52 ΩTa có R1234 = 16 Ω, vậy cách mắc này đạt yêu cầu.
Sơ đồ mạch điện:
---[R1]---[R2]--- | | ---[R3]---[R4]---Trong sơ đồ trên, dấu --- biểu thị mạch nối tiếp và dấu | biểu thị mạch song song.
Đúng 0
Bình luận (0)
Phải dùng tối thiểu bảo nhiêu điện trở loại 3 ôm để mắc thành điện trở có điện trở là 4 ôm. Cách tính và vẽ cách mắc đó
Với cách biến đổi
u
1
+
3
ln
x
thì tích phân
∫
1
e
ln
x
x
1
+
3
ln
x...
Đọc tiếp
Với cách biến đổi u = 1 + 3 ln x thì tích phân ∫ 1 e ln x x 1 + 3 ln x trở thành
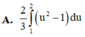
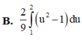
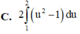
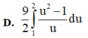
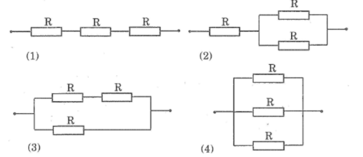
Ba điện trở cùng giá trị R = 30Ω. Có mấy cách mắc cả ba điện trở này thành một mạch điện ? Vẽ sơ đồ các cách mắc đó.
Bằng cách đặt
t
3
x
, bất phương trình
9
x
−
5.3
x
+
1
+
54
≤
0
trở thành bất phương trình nào dưới đây? A.
t
2
−
5
t
+
54
≤
0
B. ...
Đọc tiếp
Bằng cách đặt t = 3 x , bất phương trình 9 x − 5.3 x + 1 + 54 ≤ 0 trở thành bất phương trình nào dưới đây?
A. t 2 − 5 t + 54 ≤ 0
B. t 2 − 8 t + 54 ≤ 0
C. - 12 t + 54 ≤ 0
D. t 2 - 15 t + 54 ≤ 0
1, Có 3 điện trở cùng giá trị R :
a, Có mấy cách mắc 3 điện trở này thành mạch điện? Vẽ sơ đồ các mạch mắc đó
b, Tính điện trở tương đương của mỗi mạch điện
mình sẽ mô tả cách vẽ, bạn tự vẽ nhé:
C1: 3 điện trở nối tiếp
Rtđ=R1+R2+R3
C2: 3 điện trở song song
\(\dfrac{1}{Rtđ}\)=\(\dfrac{1}{R1}+\dfrac{1}{R2}+\dfrac{1}{R3}\)
C3: R1 nt (R2//R3)
Rtđ=R1+(\(\dfrac{1}{R2}+\dfrac{1}{R3}\))
C4: (R1 nt R2)//R3
Rtđ=\(\dfrac{\left(R1+R2\right)R3}{R1+R2+R3}\)
Đúng 1
Bình luận (0)
có 4 cách mắc
c1:R1ntR2ntR3
Rtd=R1+R2+R3
c2:(R1ntR2)ssR3
R12=R1+R2
\(\dfrac{1}{Rtd}\)=\(\dfrac{1}{R12}\)+\(\dfrac{1}{R3}\)\(\)
c3:R1ssR2ssR3
\(\dfrac{1}{Rtd}\)=\(\dfrac{1}{R1}\)+\(\dfrac{1}{R2}\)+\(\dfrac{1}{R3}\)
c4:R1nt(R2ssR3)
\(\dfrac{1}{R23}\)=\(\dfrac{1}{R2}\)+\(\dfrac{1}{R3}\)
Rtd=R23+R1
Đúng 0
Bình luận (0)
cách trở thành học sinh ngoan là gì
Tham khảo
1 Luôn sẵn sàng cho việc học.2 Lựa chọn phương pháp học phù hợp.3 Tập trung cao độ khi nghe giảng.4 Học cách ghi chép bài.5 Làm bài tập về nhà đúng hạn và đầy đủ6 Tìm tòi, học hỏi những nguồn kiến thức mới.7 Ôn tập bài từ sớm.8 Giữ tinh thần bình tĩnh.
Đúng 2
Bình luận (1)
Đừng ngại đặt câu hỏi. ...Hãy tập đi từng bước nhỏ ...Ghi chú lại những thứ cần thiết. ...Nghe tích cực. ...Tận dụng tất cả những “tài nguyên” mà bạn có ...Đừng quên chia sẻ với người khác những gì bạn biết. ...Học phải đi đôi với hành. ...Gạt bỏ những suy nghĩ tiêu cực.
Đúng 1
Bình luận (0)