TA
Những câu hỏi liên quan
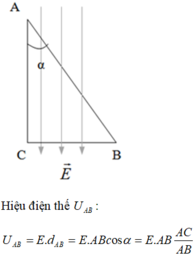
Ba điểm A, B, C tạo thành một tam giác vuông tại C, có AC=4cm, BC=3cm và nằm trong một điện trường đều. Véctơ cường độ điện trường hướng từ A đến C và có độ lớn E=5000V/m. Hiệu điện thế U A B ?
A. 100V
B. 0V
C. 200V
D. -100V
Cho tam giác ABC vuông tại B, tia phân giác của góc A cắt BC tại D. Kẻ DH vuông góc AC (H thuộc AC). Gọi I là giao điểm của AD và BC
A) giả sử AB=6cm , BC=8cm. Tính AC
B) c/m Tam giác ABD= tam giác AHD; AB=AH
C) AI vuông góc BH
D) trên tia đối BA lấy điểm K sao cho BK=CH. C/m ba điểm H,D,K thẳng hàng
Cho tam giác ABC vuông tại B, tia phân giác góc A cắt BC tại D. Kẻ DH vuông góc AC(H thuộc AC). Gọi I là giao điểm AD và BH
A) giả sử AB= 6cm; BC= 8cm. Tính AC
B) C/m tam giác ABD= tam giác AHD; AH=AB
C) C/m AI vuông góc BH
D) trên tia đối tia BA lấy K sao cho BK=CH.C/m ba điểm H,D,K thẳng hàng
Cho tam giác ABC vuông tại A
a) Cho AB=6cm,AC=8cm. Tính BC và chu vi của tam giác ABC
b) Phân giác của góc B cắt AC tại D.Kẻ DH vuông góc với BC tại H.cmr tam giác BAH cân
c) Qua C kẻ đường thẳng vuông góc với BD tại K.Cmr BA,HD,CK đồng quy tại 1 điểm
a, Áp dụng định lý Pytago vào tam giác ABC, ta có
AB2+AC2=BC2
=>36 + 64 = BC2
=>BC=10cm
Chu vi tam giác ABC là:
6+8+10=24cm
Mình làm đúng mà
Nguyễn Đăng Quang bạn còn mấy câu kia thì sau -.-
Xem thêm câu trả lời
cho tam giác ABC vuông tại A: AB=6cm; AC =8cm; góc B= 60 độ. Tia phân giác của góc B cắt AC tại E. Kẻ EH vuông BC
a): c/m: EA=EH
b) từ H kẻ đường thẳng song song với BE cắt Ac tại K. Gọi I là giao điểm của BA và HE. C/m: HK vuông IC
c) tam giác BIC là tam giác gì? Vì sao?
Cho tam giác ABC vuông tại A (AB <AC), tia phân giác của B cắt AC tại D, vẽ DE vuông góc BC tại E
a, C/m tam giác ABD = tam giác EBD
b, Cho AB=6cm, Ac= 8cm. Tính BC,EC
c, Gọi I là giao điểm của tia ED và BA, C/M tam giác BIC cân.
d, So sánh AD và DC
a) Xét tam giác ABD vuông tại A và tam giác EBD vuông tại E
có: BD là cạnh chung
góc ABD = góc EBD (gt)
\(\Rightarrow\Delta ABD=\Delta EBD\left(ch-gn\right)\)
b) ta có: \(\Delta ABD=\Delta EBD\left(pa\right)\)
=> AB = EB = 6 cm ( 2 cạnh tương ứng)
=> EB = 6 cm
Xét tam giác ABC vuông tại A
có: \(AB^2+AC^2=BC^2\left(py-ta-go\right)\)
thay số: \(6^2+8^2=BC^2\)
\(\Rightarrow BC^2=100\)
\(\Rightarrow BC=10cm\)
mà \(E\in BC\)
=> EB + EC = BC
thay số: 6 + EC = 10
EC = 10 - 6
=> EC = 4 cm
c) ta có: \(\Delta ABD=\Delta EBD\left(pa\right)\)
=> AD = ED ( 2 cạnh tương ứng)
AB = EB ( 2 cạnh tương ứng) (1)
Xét tam giác ADI vuông tại A và tam giác EDC vuông tại E
có: AD = ED ( chứng minh trên)
góc ADI = góc EDC ( đối đỉnh)
\(\Rightarrow\Delta ADI=\Delta EDC\left(cgv-gn\right)\)
=> AI = EC ( 2 cạnh tương ứng)(2)
Từ (1);(2) => AB + AI = EB + EC
=> BI = BC
=> tam giác BIC cân tại B ( định lí tam giác cân)
d) ta có: \(\Delta ABD=\Delta EBD\left(pa\right)\)
=> AD = ED ( 2 cạnh tương ứng) (1)
Xét tam giác EDC vuông tại E
có: ED < DC ( định lí cạnh góc vuông, cạnh huyền) (2)
Từ (1);(2) => AD <DC
mk ko bít kẻ hình trên này!
Đúng 1
Bình luận (0)
cho tam giác abc vuông tại a có ab=6cm ac=8cm tia phân giác của góc b cắt ac tại d . kẻ de vuông góc với bc tại e
a)tính bc
b) cm be=ba
c) cm bd là trung trực ae
d) Gọi h là hình chiếu của điểm c trên dường thẳng bd . Cm 3 đường thẳng ba,ed,ch đồng quy
Xem chi tiết
A, B, C là ba điểm tạo thành một tam giác vuông tại A, trong điện trường đều có vectơ cường độ điện trường song song với cạnh AB và có độ lớn E 104 V/m (hình vẽ). Cho AB AC 5 cm. Một prôtôn (có điện tích 1,6.10−19 C) dịch chuyển từ A đến B rồi từ B đến C. Tính công của lực điện tác dụng lên prôtôn trong hai trường hợp trên.
Đọc tiếp

A, B, C là ba điểm tạo thành một tam giác vuông tại A, trong điện trường đều có vectơ cường độ điện trường song song với cạnh AB và có độ lớn E = 104 V/m (hình vẽ). Cho AB = AC = 5 cm. Một prôtôn (có điện tích 1,6.10−19 C) dịch chuyển từ A đến B rồi từ B đến C. Tính công của lực điện tác dụng lên prôtôn trong hai trường hợp trên.
Cho tam giác AB C có AB =6cm, AC=8cm và BC=10cm. Gọi I là giao diểm ba đường phân giác. Tia BI cắt AC tại D. Chứng minh:
a, (1) Tam giác ABC vuông tại A. (2) Góc AIC bằng góc BDC
b, 5AD=3DC
Tam giác BIM vuông tại I(M là trung điểm của BC ).