Tính diện tích ngũ giác ABCDE có AB=BC=DE=CD+EA=m và góc A =góc C=90 độ
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
H24
Những câu hỏi liên quan
Tính diện tích ngũ giác ABCDE có AB=BC=DE=CD+EA=m và góc A =góc C=90 độ
Cho ngũ giác ABCDE có góc ABC = góc CDE=90 độ ; BC=CD=AE=1cm và AB+DE=1cm .Cmr:diện tích ABCDE =1cm
Cho ngũ giác lồi ABCDE có M; N; P; Q; R lần lượt là trung điểm của AB; BC; CD; DE; EA. Lấy S; X; Y; Z; T theo thứ tự là trung điểm của NR; MQ; NQ; MP; PR.
a) Hãy tìm tỉ số chu vi và tỉ số diện tích giữa 2 ngũ giác ABCDE và XTYZS ?
b) Tìm điều kiện của ngũ giác ABCDE để ngũ giác XTYZS là ngũ giác đều ? (By: 黒川猫)
Cho tam giác ABC ( góc A = 90 độ ) có AB = 9 cm, AC = 12 cm. Tia phân giác góc A cắt BC tại D. Từ D kẻ DE vuông góc với AC ( E thuộc AC ).
a) Tính độ dài của BD, CD và DE
b) Tính diện tích tam giác ADB và BCD
a) BD=45/7 CD=60/7 DE36/7
b) ADB=162/7 BCD k có vì 3 điểm này thẳng hàng
Đúng 0
Bình luận (0)
cho tam giác ABC góc A bằng 90 độ có AB=9cm AC=12cm.Tia phân giác góc A cắt BC tại D.Từ D kẻ DE vuông góc với AC (E thuộc AC)
a) Tính độ dài đoạn thẳng BD,CD và DE
b) tính diện tích tam giác ABD và ACD
Cho ngũ giác đều ABCDE. Gọi M, N, P, Q,, R tương ứng là trung điểm của các cạnh BC, CD, DE, EA, AB. Chứng minh MNPQR là ngũ giác đều.
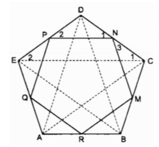
Xét △ ABC và △ BCD:
AB = BC (gt)
∠ B = ∠ C (gt)
BC = CD (gt)
Do đó: △ ABC = △ BCD (c.g.c)
⇒ AC = BD (1)
Xét △ BCD và △ CDE:
BC = CD (gt)
∠ C = ∠ D (gt)
CD = DE (gt)
Do đó: △ BCD = △ CDE (c.g.c) ⇒ BD = CE (2)
Xét △ CDE và △ DEA:
CD = DE (gt)
∠ D = ∠ E (gt)
DE = EA (gt)
Do đó: △ CDE = △ DEA (c.g.c) ⇒ CE = DA (3)
Xét △ DEA và △ EAB:
DE = EA (gt)
∠ E = ∠ A (gt)
EA = AB (gt)
Do đó: △ DEA = △ EAB (c.g.c) ⇒ DA = EB (4)
Từ (1), (2), (3), (4) suy ra: AC = BD = CE = DA = EB
Trong △ ABC ta có RM là đường trung bình
⇒ RM = 1/2 AC (tính chất đường trung bình của tam giác)
Mặt khác, ta có: Trong Δ BCD ta có MN là đường trung bình
⇒ MN = 1/2 BD (tính chất đường trung bình của tam giác)
Trong △ CDE ta có NP là đường trung bình
⇒ NP = 1/2 CE (tính chất đường trung bình của tam giác)
Trong △ DEA ta có PQ là đường trung bình
⇒ PQ = 1/2 DA (tính chất đường trung bình của tam giác)
Trong △ EAB ta có QR là đường trung bình
⇒ QR = 1/2 EB (tính chất đường trung bình của tam giác)
Suy ra: MN = NP = PQ = QR = RM
Ta có: ∠ A = ∠ B = ∠ C = ∠ D = ∠ E = ((5-2 ). 180 0 )/5 = 108 0
△ DPN cân tại D
⇒ ∠ (DPN) = ∠ (DNP) = ( 180 0 - ∠ D )/2 = ( 180 0 - 108 0 )/2 = 36 0
△ CNM cân tại C
⇒ ∠ (CNM) = ∠ (CMN) = ( 180 0 - ∠ D )/2 = ( 180 0 - 108 0 )/2 = 36 0
∠ (ADN) + ∠ (PNM) + ∠ (CNM) = 180 0
⇒ ∠ (PNM) = 180 0 - ( ∠ (ADN) + ∠ (CNM) )
= 180 0 - ( 36 0 – 36 0 ) = 108 0
△ BMR cân tại B
⇒ ∠ (BMR) = ∠ (BRM) = ( 180 0 - ∠ B )/2 = ( 180 0 - 108 0 )/2 = 36 0
∠ (CMN) + ∠ (BRM) + ∠ (BMR) = 180 0
⇒ ∠ (NMR) = 180 0 - ( ∠ (CMN) + ∠ (BMR) )
= 180 0 - ( 36 0 – 36 0 ) = 108 0
△ ARQ cân tại A
⇒ ∠ (ARQ) = ∠ (AQR) = ( 180 0 - ∠ A )/2 = ( 180 0 - 108 0 )/2 = 36 0
∠ (BRM) + ∠ (MRQ) + ∠ (ARQ) = 180 0
⇒ ∠ (MRQ) = 180 0 - ( ∠ (BRM) + ∠ (ARQ) )
= 180 0 - ( 36 0 – 36 0 ) = 108 0
△ QEP cân tại E
⇒ ∠ (EQP) = ∠ (EPQ) = ( 180 0 - ∠ E )/2 = ( 180 0 - 108 0 )/2 = 36 0
∠ (AQR) + ∠ (RQP) + ∠ (EQP) = 180 0
⇒ ∠ (RQP) = 180 0 - ( ∠ (AQR) + ∠ (EQP) )
= 180 0 - ( 36 0 – 36 0 ) = 108 0
∠ (EQP) + ∠ (QPN) + ∠ (DPN) = 180 0
⇒ ∠ (QPN) = 180 0 - ( ∠ (EPQ) + ∠ (DPN) )
= 180 0 - ( 36 0 – 36 0 ) = 108 0
Suy ra : ∠ (PNM) = ∠ (NMR) = ∠ (MRQ) = ∠ (RQP) = ∠ (QPN)
Vậy MNPQR là ngũ giác đều.
Đúng 0
Bình luận (0)
cho ngũ giác đều ABCDE đường phân giác góc A,góc B cắt nhau ở O, M là trung điểm của AB, OM=r,tính diện tích ngũ giác
cho tam giác ABC,có góc A=90 độ .AB=60cm,AC=80 cm .Từ A vẽ các đường vuông góc với các tia phân giác góc B và C tại M và N.AM,AN cắt BC lần lượt ở D và E.
Tính DE
Tính diện tích tam giác ADE
Tính diện tích DMNE
Tam giác ABC có góc A =90° ; AB =45 cm; AC = 6cm. Trên BC lấy điểm D sao cho CD = 2cm. Đường vuông góc với BC ở D cắt AC ở E.
a)Tính độ dài EC=EA
b))Tính diện tích tam giác ABC

