cho x,y là 2 số thực ≠0 thỏa mãn 2x2+ y2/4 +1/x2=4
A=2018+xy
Cho x, y là hai số thực thỏa mãn x y + ( 1 + x 2 ) ( 1 + y 2 ) = 1. Chứng minh rằng x 1 + y 2 + y 1 + x 2 = 0.
x y + ( 1 + x 2 ) ( 1 + y 2 ) = 1 ⇔ ( 1 + x ) 2 ( 1 + y ) 2 = 1 − x y ⇒ ( 1 + x 2 ) ( 1 + y 2 ) = 1 - x y 2 ⇔ 1 + x 2 + y 2 + x 2 y 2 = 1 − 2 x y + x 2 y 2 ⇔ x 2 + y 2 + 2 x y = 0 ⇔ x + y 2 = 0 ⇔ y = − x ⇒ x 1 + y 2 + y 1 + x 2 = x 1 + x 2 − x 1 + x 2 = 0
Cho x, y là các số thực dương thỏa mãn 2 ( x 2 + y 2 ) + x y = ( x + y ) ( x y + 2 ) Giá trị nhỏ nhất của biểu thức P = 4 ( x 3 y 3 + y 3 x 3 ) - 9 ( x 2 y 2 + y 2 x 2 )
A. - 25 4
B. 5
C. -13
D. - 23 4
Đáp án D
Cho x,y > 0 thỏa mãn 2 ( x 2 + y 2 ) + x y = ( x + y ) ( 2 + x y ) ⇔ 2 ( x + y ) 2 - ( 2 + x y ) ( x + y ) - 3 x y = 0 (*)
Đặt x + y = u x y = v ta đc PT bậc II: 2 u 2 - ( v + 2 ) u - 3 = 0 gải ra ta được u = v + 2 + v 2 + 28 v + 4 4
Ta có P = 4 ( x 3 y 3 + y 3 x 3 ) - 9 ( x 2 y 2 + y 2 x 2 ) = 4 ( x y + y x ) 3 - 9 ( x y + y x ) 2 - 12 ( x y + y x ) + 18 , đặt t = ( x y + y x ) , ( t ≥ 2 ) ⇒ P = 4 t 3 - 9 t 2 - 12 t + 18 ; P ' = 6 ( 2 t 2 - 3 t + 2 ) ≥ 0 với ∀ t ≥ 2 ⇒ M i n P = P ( t 0 ) trong đó t 0 = m i n t = m i n ( x y + y x ) với x,y thỏa mãn điều kiện (*).
Ta có :
t = ( x y + y x ) = ( x + y ) 2 x y - 2 = u 2 v - 2 = ( v + 2 + v 2 + 28 v + 4 ) 2 16 v - 2 = 1 16 ( v + 2 v + v + 4 v + 28 ) 2 - 2 ≥ 1 16 ( 2 2 + 32 ) 2 - 2 = 5 2
Vậy m i n P = P ( 5 2 ) = 4 . ( 5 2 ) 2 - 9 ( 5 2 ) 2 - 12 . 5 2 + 18 = - 23 4
Cho các số thực x, y dương và thỏa mãn log 2 x 2 + y 2 3 xy + x 2 + 2 log 2 x 2 + 2 y 2 + 1 ≤ log 2 8 xy .Tìm giá trị nhỏ nhất của biểu thức P = 2 x 2 - xy + 2 y 2 2 xy - y 2 .
cho 2 số x, y là 2 số thực thỏa mãn x2+y2=4. tìm giá trị lớn nhất của biểu thức M=\(\frac{xy}{x+y+4}\)
1.Cho các số thực x, y thỏa mãn x+y+4=0. Tìm GTLN của biểu thức: A= 2(x3+y3)+3(x2+y2)+10xy
Cho x y là số thực thỏa mãn x - y - xy=3 Tìm GTNN của A= x2 +y2
Cho hai số thực x≠0, y≠0 thay đổi và thỏa mãn điều kiện (x+y).xy=x2+y2–xy. Giá trị lớn nhất của biểu thức M = 1 x 3 + 1 y 3 là
A. 18
B. 1
C. 9
D. 16
Đáp án D
Phương pháp giải:
Đặt ẩn phụ, đưa về hàm một biến, dựa vào giả thiết để tìm điều kiện của biến
Lời giải:
Từ giả thiết chia cả 2 vế cho x2y2 ta được : 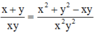
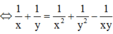
Đặt 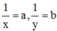 ta có
ta có ![]()
Khi đó ![]()
![]()
Ta có ![]() mà
mà 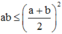
nên ![]()
![]()
![]()
Dấu đẳng thức xảy ra khi 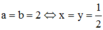 . Vậy Mmax = 16
. Vậy Mmax = 16
cho x y là 2 số thực thỏa mãn xy >=1, chung minh rang 1/1+X2+1/1+Y2>=2/1+XY
bài này ko dùng cô-si nhé, đề chỉ cho x,y là số thực và thỏa mãn \(xy\ge1\) chứ ko nói j đến dương, tham khảo bài lm của mk nhé:
BÀI LÀM
\(\frac{1}{1+x^2}+\frac{1}{1+y^2}\ge\frac{2}{1+xy}\)
\(\Leftrightarrow\)\(\frac{1}{1+x^2}-\frac{1}{1+xy}+\frac{1}{1+y^2}-\frac{1}{1+xy}\ge0\)
\(\Leftrightarrow\)\(\frac{1+xy-1-x^2}{\left(1+x^2\right)\left(1+xy\right)}+\frac{1+xy-1-y^2}{\left(1+y^2\right)\left(1+xy\right)}\ge0\)
\(\Leftrightarrow\)\(\frac{x\left(y-x\right)}{\left(1+x^2\right)\left(1+xy\right)}+\frac{y\left(x-y\right)}{\left(1+x^2\right)\left(1+xy\right)}\ge0\)
\(\Leftrightarrow\) \(\frac{x\left(y-x\right)\left(1+y^2\right)}{\left(1+x^2\right)\left(1+xy\right)\left(1+y^2\right)}+\frac{y\left(x-y\right)\left(1+x^2\right)}{\left(1+xy\right)\left(1+y^2\right)\left(1+x^2\right)}\ge0\)
\(\Leftrightarrow\)\(\frac{\left(y-x\right)\left(x+xy^2-y-x^2y\right)}{\left(1+xy\right)\left(1+x^2\right)\left(1+y^2\right)}\ge0\)
\(\Leftrightarrow\)\(\frac{\left(y-x\right)\left(x-y\right)\left(1-xy\right)}{\left(1+xy\right)\left(1+x^2\right)\left(1+y^2\right)}\ge0\)
\(\Leftrightarrow\)\(\frac{\left(x-y\right)^2\left(xy-1\right)}{\left(1+xy\right)\left(1+x^2\right)\left(1+y^2\right)}\ge0\)
đến đây bn tự giải thích và làm tiếp nhé
CÁCH 2: \(VT=\frac{1}{1+x^2}+\frac{1}{1+y^2}=\frac{2+x^2+y^2}{1+y^2+x^2+x^2y^2}\)
Ta luôn có: \(\left(a-b\right)^2\ge0\) \(\Leftrightarrow\)\(a^2-2ab+b^2\ge0\)\(\Leftrightarrow\)\(a^2+b^2\ge2ab\)
Dấu "=" xảy ra \(\Leftrightarrow\)\(a=b\)
Áp dụng BĐT trên ta có: \(x^2+y^2\ge2xy\) mà \(xy\ge1\) nên \(x^2+y^2\ge2\)
\(xy\ge1\) \(\Rightarrow\)\(\left(xy\right)^2=x^2y^2\ge1\)
Khi đó: \(VT=\frac{1}{1+x^2}+\frac{1}{1+y^2}=\frac{1+x^2+y^2}{1+x^2+y^2+x^2y^2}\ge\frac{2xy+1}{2xy+1+1}\ge\frac{2+2}{2xy+2}=\frac{4}{2\left(xy+1\right)}=\frac{2}{1+xy}\)
\(\Rightarrow\)\(VT\ge\frac{2}{1+xy}\)hay \(\frac{1}{1+x^2}+\frac{1}{1+y^2}\ge\frac{2}{1+xy}\) (đpcm)
Ta có: \(\frac{1}{1+x^2}+\frac{1}{1+y^2}\)\(=1-\frac{\left(xy-1\right)\left(xy+1\right)}{\left(xy+1\right)^2+\left(x-y\right)^2}\ge1-\frac{\left(xy-1\right)\left(xy+1\right)}{\left(xy+1\right)^2}=\frac{2}{1+xy}\)
Cho hai số thực x, y thỏa mãn x 2 + y 2 = 4 và x y = − 3 . Tính giá trị của biểu thức P= x+y
Ta có ( x + y ) 2 = x 2 + y 2 + 2 x y = 4 − 2 3 = ( 3 − 1 ) 2 ⇒ x + y = 3 − 1.
Suy ra P = x + y = 3 − 1 k h i x + y ≥ 0 1 − 3 k h i x + y < 0 .