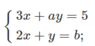
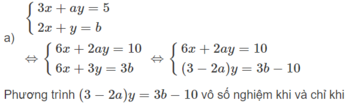
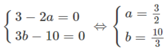
Vậy hệ phương trình đã cho vô số nghiệm khi a = 3/2, b = 10/3.

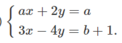
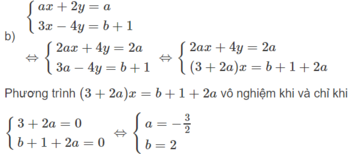
Vậy hệ phương trình đã cho vô số nghiệm khi a = -3/2, b = 2

khó quá nhờ

Để hệ phương trình  a - 2 x + 5 b y = 25 2 a x - b - 2 y = 5  có nghiệm là (x; y) = (3; -1) thì (x;y) = (3; -1) thỏa mãn hệ phương trình

Thay x = 3, y = -1 vào hệ phương trình ta được:

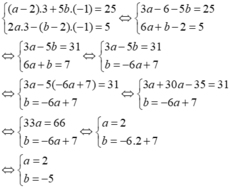
Vậy với a = 2, b = -5 thì hệ phương trình  a - 2 x + 5 b y = 25 2 a x - b - 2 y = 5  có nghiệm là (x;y) = (3; -1)

a, \(\left\{{}\begin{matrix}m^2x-my=2m\\x+my=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left(m^2+1\right)x=2m+1\\y=\dfrac{1-x}{m}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{2m+1}{m^2+1}\\y=\dfrac{1-\dfrac{2m+1}{m^2+1}}{m}\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{2m+1}{m^2+1}\\y=\dfrac{\dfrac{m^2+1-2m-1}{m^2+1}}{m}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{2m+1}{m^2+1}\\y=\dfrac{\dfrac{m^2-2m}{m^2+1}}{m}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{2m+1}{m^2}\\y=\dfrac{m^2-2m}{m^2+1}:m=\dfrac{m\left(m-2\right)}{m\left(m^2+1\right)}=\dfrac{m-2}{m^2+1}\end{matrix}\right.\)

b, Để hpt có nghiệm duy nhất khi \(\dfrac{m}{1}\ne-\dfrac{1}{m}\Leftrightarrow m^2\ne-1\left(luondung\right)\)

\(\dfrac{2m+1}{m^2}+\dfrac{m-2}{m^2+1}=-1\)

\(\Leftrightarrow\left(2m+1\right)\left(m^2+1\right)+m^2\left(m-2\right)=-m^2\left(m^2+1\right)\)

\(\Leftrightarrow2m^3+2m+m^2+1+m^3-2m^2=-m^4-m^2\)

\(\Leftrightarrow3m^3-m^2+2m+1=-m^4-m^2\)

\(\Leftrightarrow m^4+3m^3+2m+1=0\)

bạn tự giải nhé