Cho x, y ∈ Z. Hãy chứng tỏ rằng: Nếu x > y thì x – y > 0
PB
Những câu hỏi liên quan
Cho x, y ∈ Z. Hãy chứng tỏ rằng: Nếu x – y > 0 thì x > y
Áp dụng quy tắc chuyển vế trong bất đẳng thức ta có:
x – y > 0
x > 0 + y
hay x > y (điều phải chứng minh)
Đúng 0
Bình luận (0)
cho x,y thuộc Z. hãy chứng tỏ rằng :
a, nếu x-y > 0 thì x>y
b, nếu x>y thì x-y>0
a, vì x-y >0 nên x>0+y (chuyển -y từ vế trái sang vế phải) hay x>y
b, tương tự thôi (giống như phần a)
tick nha Ngọc ! (>^_^<)
Đúng 1
Bình luận (0)
Cho x , y thuộc Z. Hãy chứng tỏ rằng:
a) Nếu x - y > 0 thì x > y
b) Nếu x > y < 0 thì x- y > 0
a) Ta có:
x - y > 0
\(\Rightarrow\)x - y là số nguyên dương nên x = y + q ( q \(\in\)N* )
\(\Rightarrow\)x > y ( đpcm )
b tương tự nha
Đúng 1
Bình luận (0)
Cho x,y\(\in\)Z. Hãy chứng tỏ rằng: Nếu x > y thì x - y > 0
Cho x,y thuộc Z. Hãy chứng tỏ rằng :
a,Nếu x - y > 0 thì x > y
b, Nếu x > y thì X - y > 0
Hãy giúp mình với. Mình cảm ơn các bạn nhiều
Hãy chứng tỏ rằng với x, y thuộc Z, ta có:
a) Nếu x > y thì x - y > 0
b) Nếu x - y > 0 thì x > y
Cho x,y ∈ Z. Hãy chứng tỏ rằng:
a)Nếu x-y > 0 thì x > y;
b)Nếu x > y thì x-y > 0.
giúp mk với nha.hôm nay mình cần gấp!!!!!
a.
- Áp dụng quy tắc chuyển vế ta có:
\(x-y>0\)
\(\Leftrightarrow x>0+y\)
\(\Leftrightarrow x>y\) (đpcm)
b.
- Áp dụng quy tắc chuyển vế, ta có:
\(x>y\)
\(\Leftrightarrow x-y>0\) (đpcm)
Đúng 1
Bình luận (0)
p/s: theo mình mấy cái này chuyển vế là ra mà cần j cm đâu :v mà thoi làm như n cho dễ
a) Nếu x - y > 0 <=> x - y + y > 0 + y <=> x > y
b) Nếu x > y <=> x - y > y - y <=> x - y > 0
Đúng 1
Bình luận (0)
Giả sử x = a / m, y = b / m (a, b, m ∈ Z, m > 0) và x < y. Hãy chứng tỏ rằng nếu chọn Z = 2 a + 1 2 m thì ta có x < z < y.
Vì x < y nên 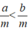 mà m > 0 nên a < b. Ta có
mà m > 0 nên a < b. Ta có
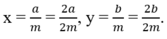
Chọn số 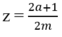 . Do 2a < 2a + 1 và m > 0 nên
. Do 2a < 2a + 1 và m > 0 nên 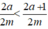 hay x < z. (1)
hay x < z. (1)
Do a < b và a; b ∈ Z nên a + 1 ≤ b suy ra 2a + 2 ≤ 2b.
Ta có 2a + 1 < 2a + 2 ≤ 2b nên 2a + 1 < 2b, do đó 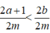 hay z < y. (2)
hay z < y. (2)
Từ (1) và (2) suy ra: x < z < y
Đúng 0
Bình luận (0)
Giả sử x = \(\dfrac{a}{m}\); y = \(\dfrac{b}{m}\)(a;b;m ϵ Z, m ≠ 0 và x < y). Hãy chứng tỏ rằng nếu chọn z = \(\dfrac{a+b}{2m}\) thì x < y < z.


