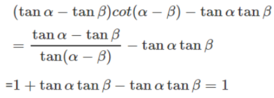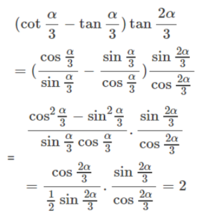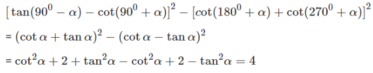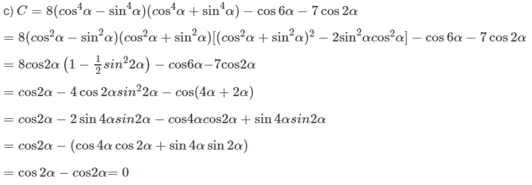Chứng minh rằng các biểu thức sau là những hằng số không phụ thuộc α, β sin6αcot3α - cos6α
PB
Những câu hỏi liên quan
Chứng minh rằng các biểu thức sau là những hằng số không phụ thuộc α, β
(tanα - tanβ)cot(α - β) - tanαtanβ
Chứng minh rằng các biểu thức sau là những hằng số không phụ thuộc α, β
(cot α/3 - tanα/3) tan2α/3
Chứng minh rằng các biểu thức sau là những hằng số không phụ thuộc α, β
[
tan
(
90
ο
-
α
)
-
c
o
t
(
90
ο...
Đọc tiếp
Chứng minh rằng các biểu thức sau là những hằng số không phụ thuộc α, β
[ tan ( 90 ο - α ) - c o t ( 90 ο + α ) ] 2 - [ c o t ( 180 ο + α ) + c o t ( 270 ο + α ) ] 2
Chứng minh rằng các biểu thức sau là những số không phụ thuộc α
C = 8 ( cos 8 α - sin 8 α ) - cos 6 α - 7 cos 2 α
Chứng minh rằng các biểu thức sau là những số không phụ thuộc α
A
2
(
sin
6
α
+
cos
6
α
)
-
3
(
sin
4
α
+
cos
4
α
)
Đọc tiếp
Chứng minh rằng các biểu thức sau là những số không phụ thuộc α
A = 2 ( sin 6 α + cos 6 α ) - 3 ( sin 4 α + cos 4 α )
A = 2 ( sin 2 α + cos 2 α ) ( sin 4 α + cos 4 α - sin 2 α cos 2 α )
- 3 ( sin 4 α + cos 4 α )
= - sin 4 α - cos 4 α - 2 sin 2 α cos 2 α
= - ( sin 2 α + cos 2 α ) 2 = - 1
Đúng 0
Bình luận (0)
Chứng minh rằng các biểu thức sau là những số không phụ thuộc α
B = 4 ( sin 4 α + sin 4 α ) - cos 4 α
A = 4 [ ( sin 2 α + cos 2 α ) 2 - 2 sin 2 α cos 2 α ] - cos4α
= 4 ( 1 - sin 2 2 α / 2 ) - 1 + 2 sin 2 2 α = 3
Đúng 0
Bình luận (0)
Tìm điều kiện của các biến trong mỗi phân thức sau đây. Chứng minh rằng khi giá trị của phân thức xác định thì giá trị đó không phụ thuộc vào các biến x và y (nghĩa là chứng tỏ rằng có thể biến đổi phân thức đã cho thành một biểu thức không chứa x và y)
2
a
x
-
2
x
-
3
y
+...
Đọc tiếp
Tìm điều kiện của các biến trong mỗi phân thức sau đây. Chứng minh rằng khi giá trị của phân thức xác định thì giá trị đó không phụ thuộc vào các biến x và y (nghĩa là chứng tỏ rằng có thể biến đổi phân thức đã cho thành một biểu thức không chứa x và y)
2 a x - 2 x - 3 y + 3 a y 4 a x + 6 x + 9 y + 6 a y (a là hằng số khác - 3/2
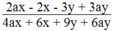 xác định khi 4ax + 6x + 9y + 6ay
≠
0
xác định khi 4ax + 6x + 9y + 6ay
≠
0
⇒ 2x(2a + 3) + 3y(2a + 3) = (2a + 3)(2x + 3y) ≠ 0
Ta có: 2a + 3 ≠ 0 ⇒ a ≠ - 3/2 ; 2x + 3y ≠ 0 ⇒ x ≠ - 3/2 y
Điều kiện: x ≠ - 3/2 y và a ≠ - 3/2
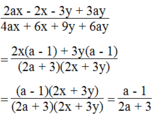
Vậy biểu thức không phụ thuộc vào x, y.
Đúng 0
Bình luận (0)
Chứng minh biểu thức sau không phụ thuộc vào biến x, y.
P = x 2 - y 2 ( x + y ) ( a y - a x ) (với a là hằng số)
Ta có:
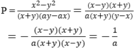
Vậy giá trị biểu thức P không phụ thuộc vào biến x, y
Đúng 0
Bình luận (0)
Cho hai mặt phẳng (α) và (β) cắt nhau theo giao tuyến m. Trên đường thẳng d cắt (α) ở A và cắt (β) ở B ta lấy hai diểm cố định
S
1
,
S
2
không thuộc (α), (β). Gọi M là một điểm di động trên (β). Giả sử các đường thẳng
M
S
1
,
M
S
2
cắt (α) lần lượt tại
M
1...
Đọc tiếp
Cho hai mặt phẳng (α) và (β) cắt nhau theo giao tuyến m. Trên đường thẳng d cắt (α) ở A và cắt (β) ở B ta lấy hai diểm cố định S 1 , S 2 không thuộc (α), (β). Gọi M là một điểm di động trên (β). Giả sử các đường thẳng M S 1 , M S 2 cắt (α) lần lượt tại M 1 và M 2 .
a) Chứng minh rằng M 1 M 2 luôn luôn đi qua một điểm cố định.
b) Giả sử đường thẳng M 1 M 2 cắt giao tuyến m tại K. Chứng minh rằng ba điểm K, B, M thẳng hàng.
c) Gọi b là một đường thẳng thuộc mặt phẳng (β) nhưng không đi qua điểm B và cắt m tại I. Chứng minh rằng khi M di động trên b thì các điểm M 1 và M 2 di động trên hai đường thẳng cố định thuộc mặt phẳng (α).
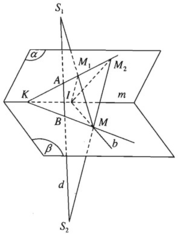
a) Mặt phẳng (M, d) cắt (α) theo giao tuyến M 1 M 2 . Điểm A cũng thuộc giao tuyến đó. Vậy đường thẳng M 1 M 2 luôn luôn đi qua điểm A cố định.
b) Mặt phẳng (M, d) cắt (β) theo giao tuyến BM. Điểm K thuộc giao tuyến đó nên ba điểm K, B, M thẳng hàng.
c) Giả sử b cắt m tại I thì mặt phẳng ( S 1 , b ) luôn luôn cắt (α) theo giao tuyến I M 1 . Do đó điểm M 1 di động trên giao tuyến của I M 1 cố định. Còn khi M di động trên b thì mặt phẳng ( S 2 , b ) cắt (α) theo giao tuyến I M 2 . Do đó điểm M 2 chạy trên giao tuyến I M 2 cố định.
Đúng 0
Bình luận (0)