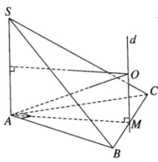
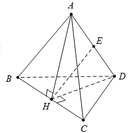
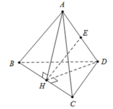
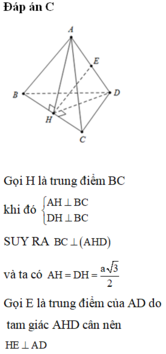
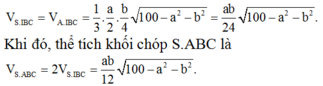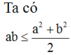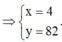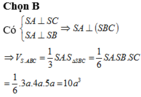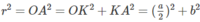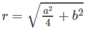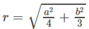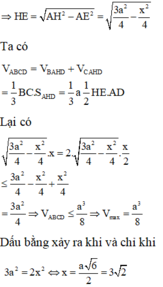Xét khối tứ diện SABC có cạnh SA, BC thỏa mãn: S A 2 + B C 2 = 18 và các cạnh còn lại đều bằng 5. Biết thể tích khối tứ diện SABC đạt giá trị lớn nhất có dạng: V m a x = x y 4 ; x , y ∈ ℕ * ; x , y = 1. Khi đó: x, y thỏa mãn bất đẳng thức nào dưới đây?
A. x + y 2 − x y > 4550.
B. x y + 2 x y > 2550.
C. x 2 − x y + y 2 < 5240.
D. x 3 − y > 19602.