Có 12 học sinh gồm 5 học sinh lớp A; 4 học sinh lớp B và 3 học sinh lớp C. Hỏi có bao nhiêu cách chọn 4 học sinh đi làm nhiệm vụ mà 4 người này không thuộc quá 2 trong 3 lớp trên?
A. 242
B. 255
C. 215
D. 220
Có 12 học sinh gồm 5 học sinh lớp A; 4 học sinh lớp B và 3 học sinh lớp C. Hỏi có bao nhiêu cách chọn 4 học sinh đi làm nhiệm vụ mà 4 người này không thuộc quá 2 trong 3 lớp trên?
A. 242
B. 255
C. 215
D. 220
Đáp án B
n ( Ω ) = C 12 4
Gọi H:” Không có quá 2 trong 3 lớp”
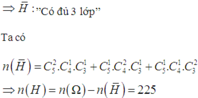
Đội thanh niên xung kích có của một trường phổ thông có 12 học sinh, gồm 5 học sinh lớp A, 4 học sinh lớp B và 3 học sinh lớp C. Cần chọn 4 học sinh đi làm nhiệm vụ sao cho 4 học sinh này thuộc không quá 2 trong ba lớp trên. Hỏi có bao nhiêu cách chọn như vậy?
A.4123
B. 3452
C. 372
D.446
TH 1: 4 học sinh được chọn thuộc một lớp:
A: có cách chọn C 5 4 = 5
B: có cách chọn C 4 4 = 1
Trường hợp này có: 6 cách chọn.
TH 2: 4 học sinh được chọn thuộc hai lớp:
A và B: có C 9 4 - ( C 5 4 + C 4 4 ) = 120
B và C: có C 9 4 - C 4 4 = 125
C và A: có C 9 4 - C 5 4 = 121
Trường hợp này có 366 cách chọn.
Vậy có 366+6=372 cách chọn thỏa yêu cầu bài toán.
Chọn C.
Xếp ngẫu nhiên 10 học sinh gồm 2 học sinh lớp 12A, 3 học sinh lớp 12 B và 5 học sinh lớp 12C thành một hàng ngang. Xác suất để trong 10 học sinh trên không có 2 học sinh cùng lớp đứng cạnh nhau bằng
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Đáp án A
Kí hiệu học sinh các lớp 12A, 12B, 12C lần lượt là A, B, C
Ta sẽ xếp 5 học sinh của lớp 12C trước, khi đó xét các trường hợp sau:
TH1: CxCxCxCxCx với x thể hiện là ghế trống. Khi đó, số cách xếp là ![]() cách.
cách.
TH2: xCxCxCxCxC giống với TH1=> có ![]() cách xếp.
cách xếp.
TH3: CxxCxCxCxC với xx là hai ghế trống liền nhau.
Chọn 1 học sinh lớp 12A và 1 học sinh lớp 12B vào hai ghế trống đó => ![]() cách xếp.
cách xếp.
Ba ghế trống còn lại ta sẽ xếp 3 học sinh còn lại của 2 lớp 12A-12B => ![]() cách xếp.
cách xếp.
Do đó, TH3 có ![]() cách xếp.
cách xếp.
Ba TH4. CxCxxCxCxC.
TH5. CxCxCxxCxC.
TH6. CxCxCxCxCxx tương tự TH3.
Vậy có tất cả ![]() cách xếp cho các học sinh.
cách xếp cho các học sinh.
Suy ra xác suất cần tính là
![]()
Đội thanh niên xung kích của một trường phổ thông gồm có 12 học sinh trong đó có 5 học sinh lớp A, 4 học sinh lớp B và 3 học sinh lớp C. Cần chọn 4 học sinh đi làm nhiệm vụ sao cho 4 học sinh này thuộc không quá hai trong ba lớp trên. Hỏi có bao nhiêu cách chọn như vậy?
A. 366
B. 2196.
C. 225.
D. 446.
Đáp án C
TH1: 4 học sinh được chọn thuộc một lớp:
+ Lớp A có C 5 4 = 5 cách chọn.
+ Lớp B có C 4 4 = 1 cách chọn.
Trường hợp này có: 6 cách chọn.
TH2: 4 học sinh được chọn thuộc 2 lớp:
+ Lớp A và B: C 9 4 − C 5 4 + C 4 4 = 120 có .
+ Lớp B và C : C 7 4 − C 4 4 = 34 có
+ Lớp C và A: C 8 4 − C 5 4 = 65 có
Trường hợp này có 219 cách chọn.
Vậy có 225 cách chọn thỏa yêu cầu bài toán.
Đội thanh niên xung kích của một trường phổ thông gồm có 12 học sinh trong đó có 5 học sinh lớp A, 4 học sinh lớp B và 3 học sinh lớp C. Cần chọn 4 học sinh đi làm nhiệm vụ sao cho 4 học sinh này thuộc không quá hai trong ba lớp trên. Hỏi có bao nhiêu cách chọn như vậy?
A. 366.
B. 2196.
C. 225.
D. 446.
ột lớp 6a có 48 học sinh gồm 3 loại : tốt , khá , đạt . trong đó số học sinh khá chiếm 5/12 số học sinh cả lớp ; số học sinh tốt bằng 75% số học sinh còn lại . tính số học sinh mỗi loại của lớp 6a ?
1+5000000:9201000*5000000000000000000000000000000000
Số hs khá: 48.5/12=20
Số hs còn tốt: (48-20).75%=21
Số hs đạt: 48-20-21=7
Số học sinh khá là:
48 x 5/12 = 20 (học sinh khá)
Số học sinh còn lại:
48 - 20 = 28 (học sinh)
Số học sinh tốt là:
28 x 75% = 21 (học sinh)
Số học sinh đạt:
48 - 21 - 20 = 7 (học sinh
Đội thanh niên xung kích của một trường phổ thông có 12 học sinh, gồm 5 học sinh lớp A, 4 học sinh lớp B và 3 học sinh lớp C. Cần chọn 4 học sinh từ đội thanh niên xung kích trên đi làm nhiệm vụ sao cho 4 học sinh này thuộc không quá hai trong ba lớp trên. Hỏi có bao nhiêu cách chọn như vậy?
A. 495
B. 252
C. 225
D. 320
Ta đếm số cách chọn 4 học sinh từ đội xung kích mà thuộc cả 3 lớp ở trên.
Phương án 1: Chọn 2 học sinh lớp A, 1 học sinh lớp B và 1 học sinh lớp C.
Số cách chọn trong trường hợp này là ![]() .
.
Phương án 2: Chọn 1 học sinh lớp A, 2 học sinh lớp B và 1 học sinh lớp C.
Số cách chọn trong trường hợp này là ![]() .
.
Phương án 3: Chọn 1 học sinh lớp A, 1 học sinh lớp B và 2 học sinh lớp C.
Số cách chọn trong trường hợp này là ![]() .
.
Theo quy tắc cộng thì số cách chọn 4 học sinh thuộc đủ cả ba lớp là 120 + 90 + 60 = 270.
Trong khi số cách chọn 4 học sinh bất kỳ từ đội xung kích là ![]() .
.
Vậy số cách chọn 4 học sinh mà các học sinh không thuộc quá hai lớp là 495 -270 =225.
Chọn C.
Một lớp học có 48 học sinh gồm ba loại : giỏi , khá và trung bình . Số học sinh trung bình chiếm 5/12 số học sinh cả lớp . Số học sinh khá bằng 4/7 số học sinh còn lại .
a. Tính số học sinh khá , số học sinh giỏi của lớp .
b. Tìm tỉ số phần trăm của số học sinh giỏi so với số học sinh của lớp .
a) Số học sinh trung bình là:
\(48.\frac{5}{12}=20\) ( học sinh )
Số học sinh còn lại là:
48 - 20 = 28 (học sinh )
Số học sinh khá là:
\(28.\frac{4}{7}=16\) ( học sinh )
Số học sinh giỏi của lớp là:
48 - 16 - 20 =12 ( học sinh )
Vậy số học sinh trung bình là 20 học sinh.
Số học sinh giói là 12 học sinh.
b) Tỉ số phần trăm số học sinh giỏi so với số học sinh cả lớp là:
12. 100% : 48 = 25%
Vậy tỉ số phần trăm giữa học sinh giởi so với cả lớp là 25%
Gọi a là số học sinh trung bình
\(\Rightarrow a=\frac{48.5}{12}=20\) (học sinh)
Gọi b là số học sinh khá (x) và học sinh giổi:
\(\Rightarrow x+a=b=48-20=28\)
\(\Rightarrow x=\frac{28.4}{7}=16\) (học sinh)
Gọi c là số học sinh giỏi:
\(\Rightarrow c=28-16=12\)
Số % học sinh giỏi là:
\(\Rightarrow\%c=\frac{12.100}{48}\%=25\%\)
Có 12 học sinh gồm 3 học sinh lớp A; 3 học sinh lớp B và 6 học sinh lớp C trong đó có hai bạn An và Bình cùng thuộc lớp C. Xếp ngẫu nhiên 12 học sinh này thành một hàng ngang, xác suất để mỗi học sinh lớp B luôn xếp giữa hai học sinh lớp C đồng thời hai bạn An và Bình luôn xếp cạnh nhau bằng
![]()
![]()
![]()
![]()