Giả sử z 1 , z 2 là hai trong số các số phức z thỏa mãn i z + 2 − i = 1 và z 1 − z 2 = 2. Giá trị lớn nhất của z 1 + z 2 bằng
A. 3
B. 2 3
C. 3 2
D. 4
Cho số phức z thỏa mãn điều kiện z - 3 + 2 i = z - i Giả sử w là số phức có môđun nhỏ nhất trong các số phức z thỏa mãn điều kiện trên. Tính môđun của w
![]()
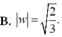
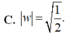
![]()
Giả sử z 1 , z 2 là hai trong số các số phức z thỏa mãn i z + 2 - i = 1 và z 1 - z 2 = 2 . Giá trị lớn nhất của z 1 + z 2 bằng
![]()
![]()
![]()
![]()
Giả sử z 1 , z 2 là hai trong số các số phức z thỏa mãn i z + 2 - i = 1 và z 1 - z 2 = 2 . Giá trị lớn nhất của z 1 + z 2 bằng
A. 4
B. 2 3
C. 3 2
D. 3
Giả sử z 1 , z 2 là hai trong số các số phức z thỏa mãn |iz + 2 - i| = 1 và | z 1 - z 2 | = 2. Giá trị lớn nhất của | z 1 | + | z 2 | bằng
A. 3.
B. 2 3
C. 3 2
D. 4.
Đáp án D.
Ta có: ![]()
![]()
![]()
=> M(x;y) biểu diễn z thuộc đường tròn tâm I(1; 2 ) bán kính R = 1
Giả sử ![]() => AB = 2 = 2R nên B là đường kính của đường tròn (I;R)
=> AB = 2 = 2R nên B là đường kính của đường tròn (I;R)
Lại có: | z 1 | + | z 2 | = OA + OB
Mặt khác theo công thức trung tuyến ta có:
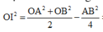
![]()
Theo BĐT Bunhiascopky ta có: ![]()
![]()
Giả sử z 1 , z 2 là hai trong số các số phức z thỏa mãn i z + 2 - i = 1 và z 1 - z 2 = 2 Giá trị lớn nhất của z 1 + z 2 bằng
A. 3
B. 2 3
C. 3 2
D. 4
Giả sử z 1 , z 2 là hai trong số các số phức z thỏa mãn i z + 2 − i = 1 và z 1 − z 2 = 2. Giá trị lớn nhất của z 1 + z 2 bằng
A. 3
B. 2 3 .
C. 3 2 .
D. 4
Đáp án D.
Ta có: i z + 2 − i = 1 ⇔ i x + y i + 2 − i = 1
(với z = x + y i x ; y ∈ ℝ )
⇔ x − 1 2 + y − 2 2 = 1 ⇒ M x ; y biểu diễn z
thuộc đường tròn tâm I 1 ; 2 bán kính R = 1.
Giả sử A z 1 ; B z 2 d o z 1 − z 2 = 2 ⇒ A B = 2 = 2 R
nên B là đường kính của đường tròn I ; R
Lại có: z 1 + z 2 = O A + O B
Mặt khác theo công thức trung tuyến ta có:
O I 2 = O A 2 + O B 2 2 − A B 2 4 ⇒ O A 2 + O B 2 = 8.
Theo BĐT Bunhiascopky ta có:
2 O A 2 + O B 2 ≥ O A + O B 2 ⇒ O A + O B ≤ 4.
Giả sử z là các số phức z thỏa mãn i z - 2 - i = 3 . Giá trị lớn nhất của biểu thức 2 z - 4 - i + z + 5 + 8 i bằng
A. 3 15
B. 15 3
C. 9 5
D. 18 5
Giả sử z là các số phức z thỏa mãn i z - 2 - i = 3 . Giá trị lớn nhất của biểu thức 2 z - 4 - i + z + 5 + 8 i bằng
![]()
![]()
![]()
![]()
Giả sử
z
1
,
z
2
là hai trong số các số phức z thỏa mãn
i
z
+
2
-
i
=
1
và
z
1
-
z
2
=
2
. Giá trị lớn nhất của ![]() bằng
bằng
A. 3
B. 2 3
C. 3 2
D. 4
Đáp án D
Phương pháp:
+) Từ giả thiết ![]() , tìm ra đường biểu diễn (C) của các số phức z.
, tìm ra đường biểu diễn (C) của các số phức z.
+) Gọi A, B lần lượt là điểm biểu diễn của ![]()
![]() vị trí của AB đối với đường tròn (C).
vị trí của AB đối với đường tròn (C).
![]()
+) Sử dụng công thức trung tuyến tính O A 2 + O B 2
+) Sử dụng BĐT Bunhiascopsky tìm GTLN của OA+OB
Cách giải:
Ta có: ![]()
với ![]()
![]()
![]() M(x;y) biểu diễn z thuộc đường tròn tâm I(
1
;
2
)bán kính R=1.
M(x;y) biểu diễn z thuộc đường tròn tâm I(
1
;
2
)bán kính R=1.
Lại có: ![]()
Mặt khác theo công thức trung tuyến ta có:
![]()
Theo BĐT Bunhiascopsky ta có:
![]()