Cho số phức z thỏa mãn z + 4 z ¯ = 7 + i ( z - 7 ) . Tính môđun của z.

Cho số phức z thỏa mãn ( 3 + i ) z - i z = 7 - 6 i . Môđun của số phức z bằng

Cho số phức z thỏa mãn z + 4 z ¯ = 7 + i ( z - 7 ) . Khi đó, môđun của z bằng bao nhiêu

A.  z = 5

B.  z = 3

C.  z = 5

D.  z = 3

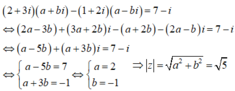
Cho số phức z thỏa mãn ( 2 + 3 i ) z - ( 1 + 2 i ) z ¯ = 7 - i . Tìm mô đun của z.

A.  z =1

B.  z =2

C.  z = 3

D.  z = 5

Cho số phức z thỏa mãn 1 - 2 i z - 7 = i . Môđun của z bằng 

A.  10

B. 10

C.  3 34 5

D. 194 5

Cho số phức z thỏa mãn z + 4 z = 7 + i z - 7 . Tính môđun của z.

A.  z = 5

B.  z = 3

C.  z = 5

D.  z = 3