Trong không gian với trục tọa độ Oxyz, cho A 0 ; 1 ; − 1 , B 1 ; 2 ; 1 , C − 2 ; 0 ; 3 . Khi đó diện tích tam giác ABC bằng bao nhiêu?
A. 101
B. 61
C. 101 2
D. 61 2
PB
Những câu hỏi liên quan
Trong không gian với hệ trục tọa độ Oxyz, cho các điểm A(-1;2;-3); B(2; -1; 0). Tọa độ của vectơ
A
B
→
là A.
A
B
→
1
;
-
1
;
1
B.
A
B
→...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho các điểm A(-1;2;-3); B(2; -1; 0). Tọa độ của vectơ A B → là
A. A B → = 1 ; - 1 ; 1
B. A B → = 1 ; 1 ; - 3
C. A B → = 3 ; - 3 ; 3
D. A B → = 3 ; - 3 ; - 3
Trong không gian với hệ trục tọa độ Oxyz, cho ba điểm A(0; 0; 2), B(3; 0; 5), C(1; 1; 0). Tọa độ của điểm D sao cho ABCD là hình bình hành là
A. D(4; 1; 3)
B. D(-4; -1; -3)
C. D(2; 1; -3)
D. D(-2; 1; -3)
Trong không gian với hệ trục tọa độ Oxyz, cho véc-tơ . Tìm tọa độ điểm A. A. A(-2;3;0) B. A(-2;0;3) C. A(0;2;-3) D. A(0;-2;3).
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho véc-tơ 
. Tìm tọa độ điểm A.
A. A(-2;3;0)
B. A(-2;0;3)
C. A(0;2;-3)
D. A(0;-2;3).
Trong không gian với hệ trục tọa độ Oxyz, cho điểm A(-3;2;-1). Tọa độ điểm A' đối xứng với A qua trục Oy là
A. A'(-3;2;1)
B. A'(3;2;-1)
C. A'(3;2;1)
D. A'(3;-2;-1)
Trong không gian với hệ trục tọa độ Oxyz, cho A(0;-1;1), B(-2;1;-1), C(-1;3;2). Biết rằng ABCD là hình bình hành, khi đó tọa độ điểm D là
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho A(0;-1;1), B(-2;1;-1), C(-1;3;2). Biết rằng ABCD là hình bình hành, khi đó tọa độ điểm D là
Trong không gian với hệ trục tọa độ Oxyz, cho A(0;-1;1),B(-2;1;-1), C(-1;3;2). Biết rằng ABCD là hình bình hành, khi đó tọa độ điểm D là: A. D(-1; 1;
2
3
) B. D(1;3;4) C. D(1;1;4) D. D(-1;-3;-2)
Đọc tiếp
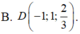
Trong không gian với hệ trục tọa độ Oxyz, cho A(0;-1;1),B(-2;1;-1), C(-1;3;2). Biết rằng ABCD là hình bình hành, khi đó tọa độ điểm D là:
A. D(-1; 1; 2 3 )
B. D(1;3;4)
C. D(1;1;4)
D. D(-1;-3;-2)
Đáp án C.
Vì ABCD là hình bình hành nên
Đúng 0
Bình luận (0)
Trong không gian với hệ trục tọa độ Oxyz, cho A(0;-1;1), B(-2;1;-1), C(-1;3;2). Biết rằng ABCD là hình bình hành, khi đó tọa độ điểm D là: A.
D
−
1
;
1
;
2
3
B.
D
1
;
3...
Đọc tiếp
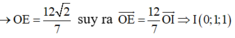
Trong không gian với hệ trục tọa độ Oxyz, cho A(0;-1;1), B(-2;1;-1), C(-1;3;2). Biết rằng ABCD là hình bình hành, khi đó tọa độ điểm D là:
A. D − 1 ; 1 ; 2 3
B. D 1 ; 3 ; 4
C. D 1 ; 1 ; 4
D. D − 1 ; − 3 ; − 2
Đáp án C
D ( x ; y ; z ) , A B → ( − 2 ; 2 ; − 2 ) , D C → ( − 1 − x ; 3 − y ; 2 − z ) A B → = D C → ⇒ D ( 1 ; 1 ; 4 )
Đúng 0
Bình luận (0)
Trong không gian với hệ trục tọa độ Oxyz , cho
a
→
-
i
→
+
2
j
→
-
3
k
→
. Tọa độ của vectơ
a
→
là: A. (2;-1;-3) B. (-3;2;-1) C. (2;-3;-1) D. (-...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz , cho a → = - i → + 2 j → - 3 k → . Tọa độ của vectơ a → là:
A. (2;-1;-3)
B. (-3;2;-1)
C. (2;-3;-1)
D. (-1;2;-3)
Trong không gian với hệ trục tọa độ Oxyz cho
a
→
-
i
→
+
2
j
→
-
3
k
→
. Tọa độ của vectơ
a
→
là: A. (2;-1;-3) B. (-3;2;-1) C. (2;-3;-1) D. (-1;2;-3)
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz cho a → = - i → + 2 j → - 3 k → . Tọa độ của vectơ a → là:
A. (2;-1;-3)
B. (-3;2;-1)
C. (2;-3;-1)
D. (-1;2;-3)
Trong không gian với hệ trục tọa độ Oxyz, cho
a
→
-
i
→
+
2
j
→
-
3
k
→
. Tọa độ của vectơ
a
→
là: A. (-3;2;-1). B. (2;-1;-3). C. (-1;2;-3). D. (2;-3;-1).
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho a → = - i → + 2 j → - 3 k → . Tọa độ của vectơ a → là:
A. (-3;2;-1).
B. (2;-1;-3).
C. (-1;2;-3).
D. (2;-3;-1).
