Ký hiệu C n k là số các tổ hợp chập k của n phần tử ( 1 ≤ k ≤ n ) . Mệnh đề nào sau đây đúng?
A. C n k = n ! k ! ( n − k ) ! .
B. C n k = k ! k ! ( n − k ) ! .
C. C n k = k ! k ! ( n − k ) ! .
D. C n k = n ! ( n − k ) ! .
Ký hiệu A n k là số các chỉnh hợp chập k của n phần tử 1 ≤ k ≤ n . Mệnh đề nào sau đây đúng?
A. A n k = n ! n + k !
B. A n k = n ! k ! n + k !
C. A n k = n ! k ! n - k !
D. A n k = n ! n - k !
Kí hiệu C n k là số tổ hợp chập k của n phần tử (0 ≤ k ≤ n). Mệnh đề nào sau đây đúng?
A . C n k = n ! ( n - k ) !
B . C n k = n ! k !
C . C n k = n ! k ! ( n - k ) !
D . C n k = n ! k ! ( n - k ) !
Kí hiệu ![]() là số các tổ hợp chập k của n phần tử (
là số các tổ hợp chập k của n phần tử (![]() ). Mệnh đề nào sau đây đúng?
). Mệnh đề nào sau đây đúng?
A. 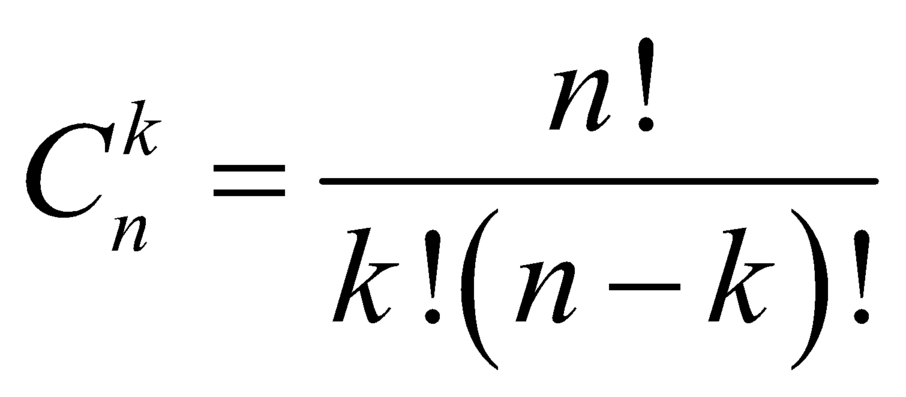 .
.
B. ![]() .
.
C. 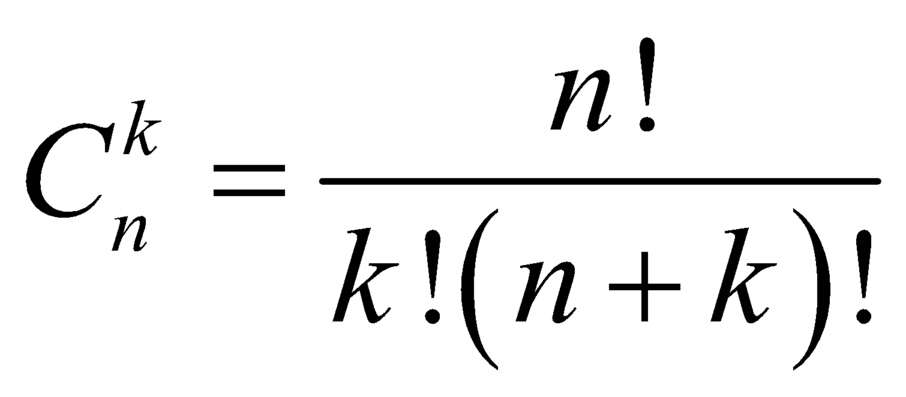 .
.
D. 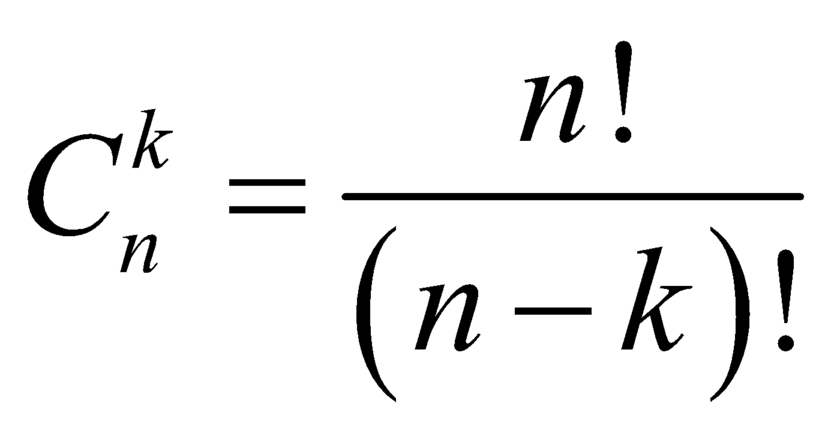 .
.
Kí hiệu A n k là số các chỉnh hợp chập k của n phần tử 1 ≤ k ≤ n . Mệnh đề nào sau đây đúng?
A. A n k = n ! n + k !
B. A n k = n ! k ! n + k !
C. A n k = n ! k ! n - k !
D. A n k = n ! n - k !
Kí hiệu A n k là số các chỉnh hợp chập k của n phần tử 1 ≤ k ≤ n . Mệnh đề nào sau đây đúng?
A. A n k = n ! ( n + k ) !
B. A n k = n ! k ! ( n + k ) !
C. A n k = n ! k ! ( n - k ) !
D. A n k = n ! ( n - k ) !
Kí hiệu A n k là số các chỉnh hợp chập k của n phần tử (1≤ k≤ n). Mệnh đề nào sau đây đúng?
A. A n k = n ! n - k !
B. A n k = n ! k ! n + k !
C. A n k = n ! k ! n - k !
D. A n k = n ! n + k !
Số các tổ hợp chập k của một tập hợp có n phần tử 1 ≤ k ≤ n là :
A . C n k = n ! ( n - k ) !
B . C n k = A n k k !
C . C n k = A n k ( n - k ) !
D . C n k = k ! ( n - k ) ! n !
Số các tổ hợp chập k của một tập hợp có n phần tử với 1 ≤ k ≤ n là
A. k ! n − k ! n !
B. A n k n − k !
C. n ! n − k !
D. A n k k !
Đáp án D
Số các tổ hợp chập k của một tập hợp có n phần tử với 1 ≤ k ≤ n là C n k = n ! k ! n − k ! = A n k k !
Viết công thức tính số chỉnh hợp chập k của n phần tử, công thức tính số tổ hợp chập k của n phần tử. Cho ví dụ.
+ Số chỉnh hợp chập k của n phần tử:
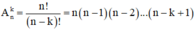
+ Số tổ hợp chập k của n phần tử:
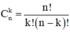
+ Ví dụ:
- Số chỉnh hợp chập 3 của 5: 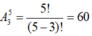
- Số tổ hợp chập 3 của 5: 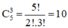
- Chọn ngẫu nhiên 5 bông hoa trong số 8 bông hoa khác nhau để cắm vào 5 lọ khác nhau:
⇒ Có 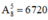 cách chọn.
cách chọn.
- Chọn ngẫu nhiên 5 bông hoa trong số 8 bông hoa khác nhau
⇒ Có 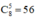 cách chọn.
cách chọn.