Trong không gian O x y z , cho mặt cầu S : x + 1 2 + y − 2 2 + z + 3 2 = 1 . Mặt cầu S có tâm I là I 1 ; − 2 ; 3
A. I 1 ; − 2 ; 3 .
B. I 1 ; 2 ; − 3 .
C. I − 1 ; 2 ; − 3 .
D. I − 1 ; 2 ; 3 .
PB
Những câu hỏi liên quan
Trong không gian Oxyz, cho mặt cầu (S):
(
x
+
3
)
2
+
(
y
+
1
)
2
+
(
z
-
1
)
2
2
. Xác định tọa độ tâm của mặt cầu A. I(-3;1;-1) B. I(3;1;-1) C. I(-3;-1;1) D. I(3;-1;1)
Đọc tiếp
Trong không gian Oxyz, cho mặt cầu (S): ( x + 3 ) 2 + ( y + 1 ) 2 + ( z - 1 ) 2 = 2 . Xác định tọa độ tâm của mặt cầu
A. I(-3;1;-1)
B. I(3;1;-1)
C. I(-3;-1;1)
D. I(3;-1;1)
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) : x²+y²+z²-2x+4z+10. Tâm của mặt cầu là điểm: A. I(1;-2;0) B. I(1;0;-2) C. I(-1;2;0) D. I(0;1;2).
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) : x²+y²+z²-2x+4z+1=0. Tâm của mặt cầu là điểm:
A. I(1;-2;0)
B. I(1;0;-2)
C. I(-1;2;0)
D. I(0;1;2).
Đáp án B
Ta có (S): (x-1)²+y²+(z+2)²=4 => (S) có tâm I(1;0;-2).
Đúng 0
Bình luận (0)
#2H3Y1-3~Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S): (x-5)² + (y-1)² + (z+2)²9. Tính bán kính R của mặt cầu (S). A. R18 B. R9 C. R3 D. R6.
Đọc tiếp
#2H3Y1-3~Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S): (x-5)² + (y-1)² + (z+2)²=9. Tính bán kính R của mặt cầu (S).
A. R=18
B. R=9
C. R=3
D. R=6.
Đáp án C
Mặt cầu (S) có tâm I(a; b; c) và bán kính R thì có phương trình (x-a)²+(y-b)²+(z-c)²=R².
Theo đề bài ta có R²=9=> R=3.
Đúng 0
Bình luận (0)
#2H3Y1-3~Trong không gian Oxyz, cho mặt cầu (S): (x-1)²+(y+2)²+z²25. Tìm tọa độ tâm I và bán kính R của mặt cầu (S). A. I(1;-2;0), R5 B. I(-1;2;0), R25 C. I(1;-2;0), R25 D. I(-1;2;0), R5.
Đọc tiếp
#2H3Y1-3~Trong không gian Oxyz, cho mặt cầu (S): (x-1)²+(y+2)²+z²=25. Tìm tọa độ tâm I và bán kính R của mặt cầu (S).
A. I(1;-2;0), R=5
B. I(-1;2;0), R=25
C. I(1;-2;0), R=25
D. I(-1;2;0), R=5.
Đáp án A
Mặt cầu (S): (x-a)²+(y-b)²+(z-c)²=R² có tâm là I(a;b;c) và bán kính là R.
Do đó, mặt cầu (S): (x-1)²+(y+2)²+z²=25 có tâm I(1;-2;0) và bán kính R=5.
Đúng 0
Bình luận (0)
Trong không gian Oxyz, cho mặt cầu
(
S
)
:
(
x
+
1
)
2
+
(
y
-
2
)
2
+
(
z
-
1
)
2
9
. Tìm tọa độ tâm I và bán kính R của mặt cầu (S). A. I(-1...
Đọc tiếp
Trong không gian Oxyz, cho mặt cầu ( S ) : ( x + 1 ) 2 + ( y - 2 ) 2 + ( z - 1 ) 2 = 9 . Tìm tọa độ tâm I và bán kính R của mặt cầu (S).
A. I(-1;2;1), R=9
B. I(1;-2;-1), R=9
C. I(1;-2;-1), R=3
D. I(-1;2;1), R=3
Trong không gian Oxyz, cho mặt cầu
(
S
)
:
(
x
+
2
)
2
+
(
y
+
1
)
2
+
(
z
-
1
)
2
12
....
Đọc tiếp
Trong không gian Oxyz, cho mặt cầu ( S ) : ( x + 2 ) 2 + ( y + 1 ) 2 + ( z - 1 ) 2 = 12 . Mặt phẳng nào sau đây cắt mặt cầu (S) theo giao tuyến là một đường tròn?
A. ( P 1 ) : x + y - z + 2 = 0
B. ( P 2 ) : x + y - z - 2 = 0
C. ( P 3 ) : x + y - z + 10 = 0
D. ( P 4 ) : x + y - z - 10 = 0
Trong không gian Oxyz, cho mặt cầu
(
S
)
:
(
x
+
2
)
2
+
(
y
+
1
)
2
+
(
z
-
1
)
2...
Đọc tiếp
Trong không gian Oxyz, cho mặt cầu ( S ) : ( x + 2 ) 2 + ( y + 1 ) 2 + ( z - 1 ) 2 = 12 . Mặt phẳng nào sau đây cắt mặt cầu (S) theo giao tuyến là một đường tròn?
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu
S
:
x
−
2
2
+
y
−
1
2
+
z
2
1...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu S : x − 2 2 + y − 1 2 + z 2 = 1 và mặt phẳng Q : 2 x − 2 y − z + 1 = 0 . Viết phương trình mặt cầu (S') đối xứng với mặt cầu (S) qua mặt phẳng (Q)
A. x + 2 3 2 + y − 7 3 2 + z − 2 3 2 = 1
B. x − 2 3 2 + y − 7 3 2 + z + 2 3 2 = 1
C. x − 2 3 2 + y + 7 3 2 + z − 2 3 2 = 1
D. x − 2 3 2 + y − 7 3 2 + z − 2 3 2 = 1
Đáp án D
Mặt cầu S 1 có tâm M(2;1;0) và có bán kính R 1 = 1
Gọi M' là hình chiếu vuông góc của M trên mặt phẳng (Q)
Ta có M M ' ⊥ Q nên đường thẳng MM' đi qua điểm M và nhận vectơ pháp tuyến của mặt phẳng (Q) làm vectơ chỉ phương.
=> phương trình tham số đường thẳng MM': x = 2 + 2 t y = 1 − 2 t z = − t , t ∈ ℝ
Vì M' là hình chiếu vuông góc của M trên mặt phẳng Q ⇒ M ' = M M ' ∩ Q
=> tọa độ điểm M' là nghiệm hệ phương trình:
2 x − 2 y − z + 1 = 0 x = 2 + 2 t y = 1 − 2 t z = − t ⇔ 2 2 + t − 2 1 − 2 t − − t + 1 = 0 x = 2 + 2 t y = 1 − 2 t z = − t ⇔ t = − 1 3 x = 4 3 y = 5 3 z = 1 3
⇒ M ' 4 3 ; 5 3 ; 1 3
Gọi I(x;y;z) là tâm của mặt cầu (S'), do mặt cầu (S') đối xứng với mặt cầu (S) qua mặt phẳng (Q) => I đối xứng với M qua mặt phẳng (Q)
=> I đối xứng với M qua mặt phẳng M'
=> M' là trung điểm của đường thẳng IM.
⇒ x = 2 x M ' − x M = 2 3 y = 2 y M ' − y M = 7 3 z = 2 z M ' − z M = 2 3 ⇒ I 2 3 ; 7 3 ; 2 3
Khi đó mặt cầu (S') có tâm I 2 3 ; 7 3 ; 2 3 , bán kính R' = R = 1 nên có phương trình:
x − 2 3 2 + y − 7 3 2 + z − 2 3 2 = 1
Đúng 0
Bình luận (0)
Trong không gian với hệ trục tọa độ Oxyz, cho mặt cầu
(
S
)
:
(
x
-
5
)
2
+
(
y
-
1
)
2
+
(
z
+
2
)
2
9
. Bán kính R của mặt cầu (S) là A. 3 B. 6 C. 9 D. 18
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho mặt cầu ( S ) : ( x - 5 ) 2 + ( y - 1 ) 2 + ( z + 2 ) 2 = 9 . Bán kính R của mặt cầu (S) là
A. 3
B. 6
C. 9
D. 18
Trong không gian Oxyz, cho điểm A(1;0;-1), mặt phẳng (P): x + y - z - 3 0. Mặt cầu (S) có tâm I nằm trên mặt phẳng (P), đi qua điểm A và gốc tọa độ O sao cho chu vi tam giác OIA bằng 6 + √2. Phương trình mặt cầu (S) là: A. (x + 2)2 + (y - 2)2 + (z + 1)2 9 và (x + 1)2 + (y - 2)2 + (z + 2)2 9 B. (x - 2)2 + (y - 2)2 + (z - 1)2 9 và x2 + y2 + (z + 3)2 9 C. (x + 2)2 + (y - 2)2 + (z + 1)2 9 và (x + 1)2 + (y - 2)2 + (z + 2)2 9 D. (x + 1)2 + (y - 2)2 + (z + 2)2 9 và (x - 2)...
Đọc tiếp
Trong không gian Oxyz, cho điểm A(1;0;-1), mặt phẳng (P): x + y - z - 3 = 0. Mặt cầu (S) có tâm I nằm trên mặt phẳng (P), đi qua điểm A và gốc tọa độ O sao cho chu vi tam giác OIA bằng 6 + √2. Phương trình mặt cầu (S) là:
A. (x + 2)2 + (y - 2)2 + (z + 1)2 = 9 và (x + 1)2 + (y - 2)2 + (z + 2)2 = 9
B. (x - 2)2 + (y - 2)2 + (z - 1)2 = 9 và x2 + y2 + (z + 3)2 = 9
C. (x + 2)2 + (y - 2)2 + (z + 1)2 = 9 và (x + 1)2 + (y - 2)2 + (z + 2)2 = 9
D. (x + 1)2 + (y - 2)2 + (z + 2)2 = 9 và (x - 2)2 + (y - 2)2 + (z - 1)2 = 9
Chọn D
Giả sử (S): x2 + y2 + z2 - 2ax - 2by - 2cz + d = 0 (a2 + b2 + c2 - d > 0)
và tâm I (a;b;c) ∈ (P) => a + b - c - 3 = 0 (1)
(S) qua A và O nên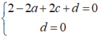 
Cộng vế theo vế (1) và (2) ta suy ra b = 2. Từ đó, suy ra I (a; 2; a-1)
Chu vi tam giác OAI bằng 6 + √2 nên OI + OA + AI = 6 + √2
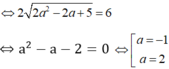
+ Với a = -1 => A (-1; 2; -2) => R = 3. Do đó:
+ Với a = 2 => I (2;2;1) => R = 3. Do đó:
Đúng 0
Bình luận (0)