Trong mặt phẳng O x y , cho điểm A 2 ; 1 và véc tơ a → 1 ; 3 . Phép tịnh tiến theo vectơ a → biến điểm A thành điểm A ' . Tọa độ điểm A ' là
A. A ' − 1 ; − 2 .
B. A ' 1 ; 2 .
C. A ' 4 ; 3 .
D. A ' 3 ; 4 .
Trong không gian Oxyz, cho điểm A(1;0;-1), mặt phẳng (P): x + y - z - 3 = 0. Mặt cầu (S) có tâm I nằm trên mặt phẳng (P), đi qua điểm A và gốc tọa độ O sao cho chu vi tam giác OIA bằng 6 + √2. Phương trình mặt cầu (S) là:
A. (x + 2)2 + (y - 2)2 + (z + 1)2 = 9 và (x + 1)2 + (y - 2)2 + (z + 2)2 = 9
B. (x - 2)2 + (y - 2)2 + (z - 1)2 = 9 và x2 + y2 + (z + 3)2 = 9
C. (x + 2)2 + (y - 2)2 + (z + 1)2 = 9 và (x + 1)2 + (y - 2)2 + (z + 2)2 = 9
D. (x + 1)2 + (y - 2)2 + (z + 2)2 = 9 và (x - 2)2 + (y - 2)2 + (z - 1)2 = 9
Chọn D
Giả sử (S): x2 + y2 + z2 - 2ax - 2by - 2cz + d = 0 (a2 + b2 + c2 - d > 0)
![]() và tâm I (a;b;c) ∈ (P) => a + b - c - 3 = 0 (1)
và tâm I (a;b;c) ∈ (P) => a + b - c - 3 = 0 (1)
(S) qua A và O nên 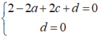
Cộng vế theo vế (1) và (2) ta suy ra b = 2. Từ đó, suy ra I (a; 2; a-1)
Chu vi tam giác OAI bằng 6 + √2 nên OI + OA + AI = 6 + √2
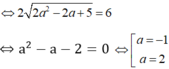
+ Với a = -1 => A (-1; 2; -2) => R = 3. Do đó:
![]()
+ Với a = 2 => I (2;2;1) => R = 3. Do đó:
![]()
Trong không gian với hệ tọa độ Oxyz, cho điểm A(1;0;-1) và mặt phẳng (P): x+ y -z -3 =0. Mặt cầu (S) có tâm I nằm trên mặt phẳng (P), đi qua điểm A và gốc tọa độ O sao cho chu vi tam giác OIA bằng 6 + 2 . Phương trình mặt cầu (S) là
A. x + 2 2 + y - 2 2 + z + 1 2 = 9 và x + 1 2 + y - 2 2 + z + 2 2 = 9
B. x - 3 2 + y - 3 2 + z - 3 2 = 9 và x - 1 2 + y - 1 2 + z + 1 2 = 9
C. x + 2 2 + y - 2 2 + z - 1 2 = 9 và x 2 + y 2 + z + 3 2 = 9
D. x + 1 2 + y - 2 2 + z + 2 2 = 9 và x - 2 2 + y - 2 2 + z - 1 2 = 9
Đáp án D.
![]()
![]()
![]()
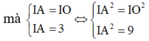
![]()
![]()
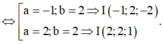
Vậy phương trình mặt cầu cần tìm là
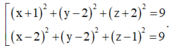
Trong không gian với hệ trục Oxyz cho điểm A(2;1;3) và đường thẳng có phương trình ( d ) : x - 1 2 = y - 2 - 1 = z 1 . Mặt phẳng (P) chứa A và d. Viết phương trình mặt cầu tâm O tiếp xúc với mặt phẳng (P).
A. x 2 + y 2 + z 2 = 12 5
B. x 2 + y 2 + z 2 = 3
C. x 2 + y 2 + z 2 = 6
D. x 2 + y 2 + z 2 = 24 5
Đáp án D.
( d ) : x - 1 2 = y - 2 - 1 = z 1 đi qua B(1;2;0) có vecto chỉ phương n d → = 2 ; - 1 ; 1
Với B A → = 1 ; - 1 ; 3 , vecto pháp tuyến của (P) là: B A → , u d → = 2 ; 5 ; 1
⇒ P : 2 x - 2 + 5 y - 1 + z - 3 = 0 ⇔ 2 x + 5 y + z - 12 = 0
Bán kính của mặt cầu cần tìm là d O , P = 2 30 5 .
Trong không gian với hệ tọa độ Oxyz, cho điểm A(2;1;3) và đường thẳng d có phương trình x - 1 2 = y - 2 - 1 = z z . Mặt phẳng chứa A và d. Viết phương trình mặt cầu tâm O tiếp xúc với mặt phẳng (P).
A. x 2 + y 2 + z 2 = 12 5 .
B. x 2 + y 2 + z 2 = 3 .
C. x 2 + y 2 + z 2 = 6 .
D. x 2 + y 2 + z 2 = 24 5 .
1. Trong mặt phẳng Oxy, có trọng tâm G(1,-1), M(2,1) và N(4,-2) lần lượt là trung điểm của AB, BC. Tìm tọa độ điểm B
2. Trong mặt phẳng Oxy, cho A(1,3), B(-2,2). Biết đường thẳng AB cắt trục tung tại điểm M(0,b). Giá trị b thuộc khoảng nào
3. Trong mặt phẳng tọa độ Oxy, cho A thỏa vecto OA= 2vecto i + 3vecto j. Tọa độ điểm A là
4. Trong mặt phẳng Oxy, cho vecto x=(1,2), vecto y=(3,4), vecto z=(5,-1). Tọa độ vecto u = 2vecto x + vecto y - vecto z là
5. Trong mặt phẳng tọa độ Oxy, cho M(2,-3), N(4,7). Tọa độ trung điểm I của đoạn thẳng MN là
6. Cho vecto x=(-4,7) và hai vecto a=(2,-1), b=(-3,4). Nếu vecto x = m vecto a + n vecto b thì m, n là cặp số nào
Trong không gian Oxyz, cho hai mặt phẳng ( P ) : x - y - 6 = 0 và (Q). Biết rằng điểm H ( 2 ; - 1 ; - 2 ) là hình chiếu vuông góc của gốc tọa độ O ( 0 ; 0 ; 0 ) xuống mặt phẳng (Q). Số đo góc giữa mặt phẳng (P) và mặt phẳng (Q) bằng
![]()
![]()
![]()
![]()
Trong mặt phẳng tọa độ Oxy, cho hai điểm A(2; 1), B(3; 3).
a) Các điểm O, A, B có thẳng hàng hay không?
b) Tìm điểm M(x; y) để OABM là một hình hành.
Tham khảo:
a) Ta có: \(\overrightarrow {OA} = \left( {2;1} \right)\) ( do A(2; 1)) và \(\overrightarrow {OB} = \left( {3;3} \right)\) (do B (3; 3)).
Hai vectơ này không cùng phương (vì \(\frac{2}{3} \ne \frac{1}{3}\)).
Do đó các điểm O, A, B không cùng nằm trên một đường thẳng.
Vậy chúng không thẳng hàng.
b) Các điểm O, A, B không thẳng hàng nên OABM là một hình hành khi và chỉ khi \(\overrightarrow {OA} = \overrightarrow {MB} \).
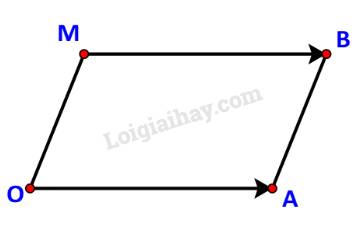
Do \(\overrightarrow {OA} = \left( {2;1} \right),\quad \overrightarrow {MB} = \left( {3 - x;3 - y} \right)\) nên
\(\overrightarrow {OA} = \overrightarrow {MB} \Leftrightarrow \left\{ \begin{array}{l}2 = 3 - x\\1 = 3 - y\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 1\\y = 2\end{array} \right.\)
Vậy điểm cần tìm là M (1; 2).
1. Trong mặt phẳng tọa độ Oxy, cho hai điểm A(0;2), B(4;2). Tìm điểm M trên đoạn thẳng AB để parabol (P) đỉnh O và đi qua điểm M chia tam giác vuông OAB thành hai phần có diện tích bằng nhau.
2. Cho hình phẳng (H ) giới hạn bởi các đường \(y=x^2,y=2x\) . Gọi S là tập hợp các giá trị của tham số thực k để đường thẳng x = k2 chia hình phẳng (H) thành hai phần có diện tích bằng nhau. Hỏi tập hợp S có bao nhiêu phần tử?
Trong không gian cho điểm A(1;0;2), mặt phẳng (P): x-y+z-2=0 và mặt cầu (S): x2+ (y-2)2+ (z+1)2 = 25. Gọi M là một điểm di động trên mặt cầu (S) và N là điểm nằm trên mặt phẳng (P) sao cho A là trung điểm của MN. Quỹ tích điểm N là đường cong có độ dài nằm trong khoảng nào dưới đây?
A. (5;12)
B. (12;16)
C. (16;20)
D. (20;24)
Trong hệ trục toạ độ Oxyz, cho điểm H(2;1;2). Điểm H là hình chiếu vuông góc của gốc toạ độ O xuống mặt phẳng (P), số đo góc giữa mặt phẳng (P) và mặt phẳng (Q): x+y-11=0 là
A. 90 °
B. 30 °
C. 60 °
D. 45 °