Nếu số phức z thỏa mãn |z|=2 và z không phải số thực thì 1 2 − z có phần thực bằng
A. 1 2
B. 1 4
C. 4
D. không xác định được giá trị chính xác.
Nếu số phức z thỏa mãn z = 2 và z không phải số thực thì 1 2 - z có phần thực bằng
A. 1 2
B. 1 4
C. 4
D. không xác định được giá trị
Nếu số phức z thỏa mãn |z| = 2 và z không phải số thực thì 1 2 − z có phần thực bằng
A. 1 2
B. 1 4
C. 4
D. không xác định được giá trị chính xác.
Nếu số phức z≠1 thỏa mãn |z|=1 thì phần thực của số phức 1 1 - z bằng
A. 1
B. 2
C. -1/2
D. 1/2
Nếu số phức z ≠ 1 thỏa mãn z = 1 thì phần thực của số phức 1 1 − z bằng
A. 1
B. − 1 2
C. 1 2
D. 2
Gọi số phức z = a + b i ( a , b ∈ ℝ ) thỏa mãn z - 1 = 1 và ( 1 + i ) ( z ¯ - 1 ) có phần thực bằng 1 đồng thời z không là số thực. Khi đó a.b bằng
A. ab=-2
B. ab=2
C. ab=1
D. ab=-1
Đáp án C
Phương pháp
Gọi số phức đã cho có dạng ![]() . Sử dụng giả thiết để đưa ra một hệ cho a, b giải trực tiếp hệ này để tìm a, b
. Sử dụng giả thiết để đưa ra một hệ cho a, b giải trực tiếp hệ này để tìm a, b
Lời giải chi tiết.
Ta có: ![]()
Do z không là số thực nên ta phải có b ≠ 0 (2)
Ta lại có
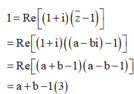
Từ (1), (2), (3) ta có hệ
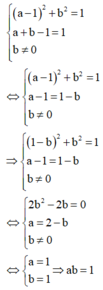
Gọi số phức z= a+bi (a,b∈ R) thỏa mãn |z-1|= 1 và ( 1 + i ) ( z ¯ - 1 ) có phần thực bằng 1 đồng thời z không là số thực. Khi đó a.b bằng
A. ab= -2
B. ab= 2
C. ab= 1
D. ab= -1
Gọi số phức z=a+bi (a,b ∈ ℝ ) thỏa mãn z - 1 = 1 v à ( 1 + i ) ( z ¯ - 1 ) có phần thực bằng 1 đồng thời z không là số thực. Khi đó a.b bằng:
![]()
![]()
![]()
![]()
Gọi số phức z = a + bi(a,b ∈ ℝ ) thỏa mãn |z-1| = 1 và (1+i)( z ¯ -1) có phần thực bằng 1 đồng thời z không là số thực. Khi đó a.b bằng
A. a.b = 1
B. a.b = 2
C. a.b = -2
D. a.b = -1
Đáp án A
Ta có 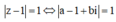
![]()
Số phức ![]()
![]()
có phần số thực bằng a+b-1 = 1(2)
Từ (1), (2) 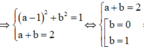
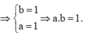
Gọi số phức z = a + bi thỏa mãn z - 1 = 1 và 1 + i z - 1 có phần thực bằng 1 đồng thời z không là số thực. Khi đó a.b bằng
A. ab = -2
B. ab = 2
C. ab = 1
D. ab = -1