Tìm số nghiệm nguyên của bất phương trình log 5 2 3 x − 2 log 2 4 − x − log 4 − x 2 + 1 > 0.
A. 3
B. 1
C. 0
D. 2
PB
Những câu hỏi liên quan
Tìm số nghiệm nguyên của bất phương trình
log
5
2
3
x
-
2
log
2
(
4
-
x
)
-
log...
Đọc tiếp
Tìm số nghiệm nguyên của bất phương trình log 5 2 3 x - 2 log 2 ( 4 - x ) - log ( 4 - x ) 2 + 1 > 0
A. 3
B. 1
C. 0
D. 2
Tìm số nghiệm nguyên của bất phương trình
log
5
2
(
3
x
-
2
)
log
2
(
4
-
x...
Đọc tiếp
Tìm số nghiệm nguyên của bất phương trình log 5 2 ( 3 x - 2 ) log 2 ( 4 - x ) - log ( 4 - x ) 2 + 1 > 0
A. 3
B. 1
C. 0
D. 2
Số nghiệm nguyên của bất phương trình
log
(
2
x
2
-
15
x
+
37
)
≤
1
là A. 4 B. 2 C. 1 D. 3
Đọc tiếp
Số nghiệm nguyên của bất phương trình log ( 2 x 2 - 15 x + 37 ) ≤ 1 là
A. 4
B. 2
C. 1
D. 3
Tìm tập nghiệm của bất phương trình log ( x - 21 ) < 2 - log x
A. (-4; 25)
B. (0; 25)
C. (21; 25)
D. (25; +∞)
H24
SGK Kết nối tri thức và cuộc sống
15 tháng 8 2023 lúc 19:47
Cho đồ thị của hàm số \(y = {\log _2}x\) và y = 2 như Hình 6.8. Tìm khoảng giá trị của x mà đồ thị hàm số \(y = {\log _2}x\) nằm phía trên đường thẳng y = 2 và từ đó suy ra tập nghiệm của bất phương trình \({\log _2}x > 2.\)
Khoảng giá trị của x mà đồ thị hàm số \(y=log_2x\) nằm phía trên đường thẳng y = 2 là \(\left(4;+\infty\right)\)
\(\Rightarrow\) Tập nghiệm của bất phương trình \(log_2x>2\) là \(\left(4;+\infty\right)\)
Đúng 0
Bình luận (0)
Tập nghiệm của bất phương trình log(x2 + 25) > log(10x) là
Tập nghiệm của bất phương trình
log
2
x
-
1
≥
log
x
là
Đọc tiếp
Tập nghiệm của bất phương trình log 2 x - 1 ≥ log x là
Tập nghiệm của bất phương trình
log
(
x
2
-
4
)
log
(
3
x
)
là:
Đọc tiếp
Tập nghiệm của bất phương trình
log ( x 2 - 4 ) > log ( 3 x ) là:
Có bao nhiêu số nguyên m trong đoạn
-
2000
;
2000
sao cho bất phương trình
10
x
m
+
log
x
10
≥
10...
Đọc tiếp
Có bao nhiêu số nguyên m trong đoạn - 2000 ; 2000 sao cho bất phương trình 10 x m + log x 10 ≥ 10 11 10 log x có nghiệm đúng với mọi x ∈ 1 ; 1000 .
A. 2000.
B. 4000.
C. 2001.
D. 4001.
Tìm số nghiệm nguyên của bất phương trình 25 - x 2 log 2 x 2 - 4 x + 5 ≤ 0
A. 6
B. 5
C. 4
D. 3
Đáp án D
Phương pháp:
- Tìm TXĐ
- Giải bất phương trình và tìm số nghiệm nguyên.
Cách giải:
Điều kiện xác định:
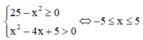
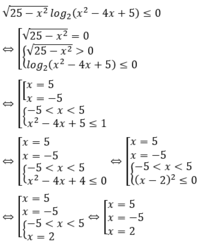
Vậy bất phương trình có 3 nghiệm nguyên.
Đúng 0
Bình luận (0)