Cho số phức z thỏa điều kiện z + 2 = z + 2 i . Giá trị nhỏ nhất của biểu thức P = z − 1 − 2 i + z − 3 − 4 i + z − 5 − 6 i được viết dưới dạng ( a + b 17 ) / 2 với a, b là các hữu tỉ. Giá trị của a + b là
A. 4
B. 2
C. 7
D. 3
Cho số phức z thỏa mãn điều kiện ( 3 + 2 i ) z + ( 2 - i ) 2 = 4 + i . Tìm phần ảo của số phức w = ( 1 + + z ) z ¯ .
A. -2
B. 0.
C. -1
D. 1
Cho số phức z thỏa mãn điều kiện ( 3 + 2 i ) z + ( 2 - i ) 2 = 4 + i . Tìm phần ảo của số phức w = ( 1 + z ) z ¯ .
![]()
![]()
![]()
![]()
Cho số phức z thỏa mãn điều kiện z - 1 = 2 . Tìm giá trị lớn nhất của T = z + i + z - 2 - i
A. m a x T = 8 2
B. m a x T = 4
C. m a x T = 4 2
D. m a x T = 8 2
Cho số phức z thỏa mãn điều kiện z - 3 + 2 i = z - i Giả sử w là số phức có môđun nhỏ nhất trong các số phức z thỏa mãn điều kiện trên. Tính môđun của w
![]()
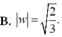
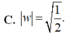
![]()
Cho số phức z thỏa mãn điều kiện z - 1 = 2 . Tìm giá trị lớn nhất của biểu thức T = z + i + z - 2 - i
![]()
![]()
![]()
![]()
Tập hợp các điểm z thỏa mãn điều kiện z - 1 = 2 là đường tròn (C) tâm I(1;0) bán kính R = 2
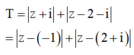
Gọi M là điểm biểu diễn cho số phức z, A(0,-1) là điểm biểu diễn cho số phức -i, B(2;1)là điểm biểu diễn cho số phức 2+i

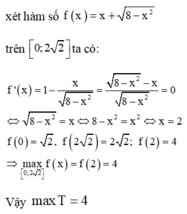
Đáp án D
Cho số phức z thỏa mãn điều kiện z - 1 = 2 .
Tìm giá trị lớn nhất của biểu thức T = z + i + z - 2 - i
A. maxT= 8 2
B. maxT=8
C. maxT= 4 2
D. maxT=4
Đáp án D
Phương pháp: Đưa biểu thức T về dạng biểu thức vector bằng cách tìm các vecto biểu diễn cho các số phức.
Cách giải:
Tập hợp các điểm z thỏa mãn điều kiện ![]() là đường tròn (C) tâm I(1;0) bán kính R=
2
là đường tròn (C) tâm I(1;0) bán kính R=
2
![]()
Gọi M là điểm biểu diễn cho số phức z, A(0;-1) là điểm biểu diễn cho số phức -i, B(2;1) là điểm biểu diễn cho số phức 2+i
Dễ thấy A,B
∈
C và ![]()
![]() AB là đường kính của đường tròn (C)
AB là đường kính của đường tròn (C)
![]() vuông tại M
vuông tại M
![]()
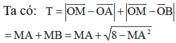
Đặt ![]()
Xét hàm số ![]() trên
trên ![]() ta có:
ta có:
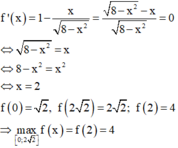
Vậy maxT=4
Cho số phức z thỏa mãn điều kiện (1 - i)(2 + i)z + 1 - i = (5 - i)(1 + i). Tính môđun của số phức w = 1 + 2 z + z 2
A. 8
B. 64
C. 2 2
D. 5
Đáp án A
Ta có z = 5 - i 1 + i + i - 1 1 - i 2 + i = 1 + 2 i ⇒ w = 8 i ⇒ w = 8 .
Cho số phức z thỏa mãn điều kiện z - 1 - i + z + 1 + 3 i = 6 5 .
Giá trị lớn nhất của z - 2 - 3 i là
A. 4 5
B. 2 5
C. 6 5
D. 5 5
Đáp án D
Phương pháp:
- Biểu diễn số phức và giải bài toán tìm GTLN trên mặt phẳng tọa độ.
Cách giải: Gọi I(1;1), J(-1;-3), A(2;3).
Xét số phức ![]() , có điểm biểu diễn là M(x;y)
, có điểm biểu diễn là M(x;y)
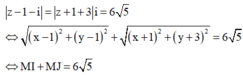
![]() M di chuyển trên đường elip có tiêu điểm I và J, độ dài trục lớn là
3
5
M di chuyển trên đường elip có tiêu điểm I và J, độ dài trục lớn là
3
5
Tìm giá trị lớn nhất của ![]() tức là tìm độ dài lớn nhất của đoạn AM khi M di chuyển trên elip.
tức là tìm độ dài lớn nhất của đoạn AM khi M di chuyển trên elip.
Ta có:
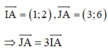
điểm A nằm trên trục lớn của elip.
![]() AM đạt độ dài lớn nhất khi và chỉ khi M trùng với B, là đỉnh của elip nằm trên trục lớn và khác phía A so với điểm I.
AM đạt độ dài lớn nhất khi và chỉ khi M trùng với B, là đỉnh của elip nằm trên trục lớn và khác phía A so với điểm I.
Gọi S là trung điểm của IJ
![]() S(0;-1)
S(0;-1)
Độ dài đoạn AB=SA+SB
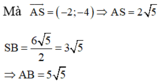
Vậy ![]()
Cho số phức z thỏa mãn điều kiện z - 1 - i + z + 1 + 3 i = 6 5 . Giá trị lớn nhất của z - 2 - 3 i là
![]()
![]()
![]()
![]()
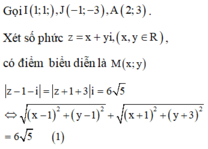
↔ M I + M J = 6 5 nên M di chuyển trên đường elip có tiêu điểm I và J, độ dài trục lớn là 3 5
Tìm giá trị lớn nhất của z - 2 - 3 i tức là tìm độ dài lớn nhất của đoạn AM khi M di chuyển trên elip
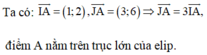
AM đạt độ dài lớn nhất khi và chỉ khi M trùng với B, là đỉnh của elip nằm trên trục lớn và khác phía A so với điểm I.

Đáp án D
Cho số phức z thỏa mãn điều kiện z - 1 - i + z + 1 + 3 i = 6 5 . Giá trị lớn nhất của z - 2 - 3 i là
A. 4 5
B. 2 5
C. 6 5
D. 5 5
Đáp án D
Phương pháp:
- Biểu diễn số phức và giải bài toán tìm GTLN trên mặt phẳng tọa độ.
Cách giải: Gọi I(1;1), J - 1 ; - 3 , A(2;3)
Xét số phức z = x + yi, (x,y ∈ R), có điểm biểu diễn là M(x;y)
![]()
![]()
![]() (1)
(1)
![]() => M di chuyển trên đường elip có tiêu điểm I và J, độ dài trục lớn là
3
5
=> M di chuyển trên đường elip có tiêu điểm I và J, độ dài trục lớn là
3
5
Tìm giá trị lớn nhất của z - 2 - 3 i tức là tìm độ dài lớn nhất của đoạn AM khi M di chuyển trên elip
Ta có: I A → = ( 1 ; 2 ) , J A → = 3 ; 6 => J A → = 3 I A → ,điểm A nằm trên trục lớn của elip.
=>AM đạt độ dài lớn nhất khi và chỉ khi M trùng với B, là đỉnh của elip nằm trên trục lớn và khác phía A so với điểm I.
Gọi S là trung điểm của IJ => S(0; - 1)
Độ dài đoạn AB = SA + SB
Mà A S → = - 2 ; - 4 => AS = 2 5 , SB = 6 5 2 = 3 5 => AB = 5 5
Vậy z - 2 - 3 i m a x = 5 5