Cho hàm số f(x) xác định trên ℝ \ − 2 ; 1 thỏa mãn f ' x = 1 x 2 + x − 2 ; f 0 = 1 3 , và f − 3 − f 3 = 0. Tính giá trị của biểu thức T = f − 4 + f − 1 − f 4
A. 1 3 ln 2 + 1 3
B. ln 80 + 1
C. 1 3 ln 4 5 + ln 2 + 1
D. 1 3 ln 8 5 + 1
Cho hàm số y = f(x) xác định trên ℝ và có đạo hàm f '(x) thỏa mãn f ' x = 1 - x x + 2 . g x + 2018 trong đó g x < 0 , ∀ x ∈ ℝ . Hàm số y = f 1 - x + 2018 x + 2019 nghịch biến trên khoảng nào?
A. 1 ; + ∞
B. 0 ; 3
C. - ∞ ; 3
D. 3 ; + ∞
Đáp án D
Ta có y ' = f 1 - x + 2018 x + 2019 ' = 1 - x ' . f ' 1 - x + 2018 = - f ' 1 - x + 2018
= - x 3 - x . g 1 - x - 2018 + 2018 = - x 3 - x . g 1 - x mà g 1 - x < 0 ; ∀ x ∈ ℝ
Nên y ' < 0 ⇔ - x 3 - x . g 1 - x < 0 ⇔ x 3 - x . g 1 - x > 0 ⇔ x 3 - x < 0 ⇔ [ x > 3 x < 0
Khi đó, hàm số y = f 1 - x + 2018 x + 2019 nghịch biến trên khoảng 3 ; + ∞
Cho hàm số y=f(x) xác định trên ℝ \ 1 , liên tục trên mỗi khoảng xác định và có bảng biến thiên như hình vẽ
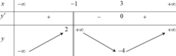
Hàm số y = f ( x ) có bao nhiêu điểm cực trị?
A. 4.
B. 3.
C. 2.
D. 5.
Đáp án A
Từ bảng biến thiên của hàm số y=f(x), suy ra bảng biến thiên của hàm số y = f ( x ) là
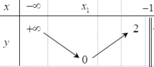

Dựa vào bảng biến thiên, ta suy ra hàm số có 4 điểm cực trị.
Cho hàm số y = f(x) xác định trên ℝ , thỏa mãn f x > 0 , ∀ x ∈ ℝ và f’(x) + 2f(x) = 0. Tính f(-1), biết rằng f(1) = 1.
A. e - 2
B. e 3
C. e 4
D. 3
Chọn C.
Ta có f ' x + 2 f x = 0 ⇔ f ' x = - 2 f x ⇔ f ' x f x = - 2 d o f x > 0
Lấy tích phân hai vế, ta được
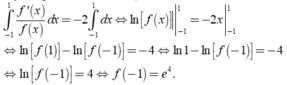
Cho hàm số f x = 2 x − 1 x + 1 xác định trên ℝ \ 1 . Đạo hàm của hàm số f(x) là:
A. f ' x = 1 x + 1 2
B. f ' x = 2 x + 1 2
C. f ' x = − 1 x + 1 2
D. f ' x = 3 x + 1 2
Đáp án D
f x = 2 x − 1 x + 1 f ' x = 2.1 − − 1 .1 x + 1 2 = 3 x + 1 2
Cho hàm số f(x) xác định trên ℝ \ 0 , thỏa mãn f ' x = 1 x 3 + x 5 , f 1 = a và f(-2) = b. Tính f - 1 + f 2
A.f(-1) + f(2) = -a - b
B. f(-1) + f(2) = a - b
C. f(-1) + f(2) = a + b
D. f(-1) + f(2) = b - a
Cho hàm số y = f(x) xác định trên ℝ và có đồ thị của hàm số f ' ( x ) , biết f ( 3 ) + f ( 2 ) = f ( 0 ) + f ( 1 ) và các khẳng định sau:
Hàm số y = f(x) có 2 điểm cực trị.
Hàm số y = f(x) đồng biến trên khoảng ( - ∞ ; 0 ) .
Max [ 0 ; 3 ] f ( x ) = f ( 3 ) .
Min ℝ f ( x ) = f ( 2 ) .
Max [ - ∞ ; 2 ] f ( x ) = f ( 0 ) .

Số khẳng định đúng là
A. 2.
B. 3.
C. 4.
C. 4.
Chọn C.
Dựa vào đồ thị hàm số f ' ( x ) suy ra BBT của hàm số y = f(x)

Khẳng định 1, 2, 5 đúng, khẳng định 4 sai.
Xét khẳng định 3: Ta có:
f ( 3 ) + f ( 2 ) = f ( 0 ) + f ( 1 ) ⇒ f ( 3 ) - f ( 0 ) = f ( 1 ) - f ( 2 ) > 0
Do đó f ( 3 ) > f ( 0 ) ⇒ Vậy khẳng định 3 đúng.
Cho hàm số y=f(x) xác định trên ℝ và có đồ thị của hàm số f’(x) và các khẳng định sau:
(1). Hàm số y=f(x) đồng biến trên khoảng 1 ; + ∞
(2). Hàm số y=f(x) nghịch biến trên khoảng - ∞ ; - 2
(3). Hàm số y=f(x) nghịch biến trên khoảng - 2 ; 1 .
(4). Hàm số y = f x 2 đồng biến trên khoảng - 1 ; 0
(5). Hàm số y = f x 2 nghịch biến trên khoảng (1;2)

Số khẳng định đúng là
A. 4
B. 3
C. 2
D. 5
Cho hàm số f(x) có đạo hàm f'(x) xác định, liên tục trên ℝ và có đồ thị f'(x) như hình vẽ bên. Hàm số y = f(x) đồng biến trên khoảng nào dưới đây?

![]()
![]()
![]()
![]()
Cho hàm số y=f(x) xác định trên ℝ và có đồ thị của hàm số f'(x), biết f(3)+f(20=f(0)+f(1) và các khẳng định sau:
1) Hàm số y=f(x) có 2 điểm cực trị
2) Hàm số y=f(x) đồng biến trên khoảng - ∞ ; 0
3) M a x 0 ; 3 f x = f 3
4) M a x ℝ f x = f 2
5) M a x - ∞ ; 2 f x = f 0 .
Số khẳng định đúng là

A. 2
B. 3
C. 4
D. 5
Cho hàm số y = f(x) xác định trên R và có đạo hàm y = f '(x) thỏa mãn f ' x = 1 − x x + 2 . g x + 2018 trong đó g x < 0 , ∀ x ∈ ℝ . Hàm số y = f 1 − x + 2018 x + 2019 nghịch biến trên khoảng nào?
A. 1 ; + ∞ .
B. (0;3)
C. − ∞ ; 3 .
D. 3 ; + ∞ .