Viết tiếp vào chỗ chấm
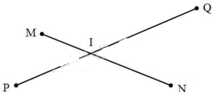
Đoạn thẳng MN cắt đoạn thẳng PQ tại điểm …..
Viết tiếp vào chỗ chấm:
a) Đoạn thẳng AB cắt đoạn thẳng CD tại điểm ....
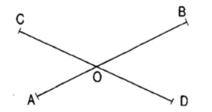
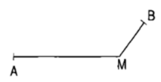
b) Đoạn thẳng AM cắt đoạn thẳng MB tại điểm ....
Phương pháp giải:
Quan sát hình ảnh, tìm hai đoạn thẳng cắt nhau tại điểm nào rồi điền tên điểm vào chỗ trống.
Lời giải chi tiết:
a) Đoạn thẳng AB cắt đoạn thẳng CD tại điểm O.
b) Đoạn thẳng AM cắt đoạn thẳng MB tại điểm M.
a) Vẽ đoạn thẳng AB và đoạn thẳng CD.

b) Đoạn thẳng AB cắt đoạn thẳng CD tại một điểm. Hãy ghi tên điểm đó rồi viết tiếp vào chỗ chấm:
Đoạn thẳng AB cắt đoạn thẳng CD tại một điểm .....
Phương pháp giải:
- Dùng bút chì và thước kẻ, nối hai điểm A và B; C và D.
- Tìm giao điểm của hai đoạn thẳng; đặt tên rồi điền vào chỗ trống.
Lời giải chi tiết:
a) Vẽ đoạn thẳng AB và đoạn thẳng CD.
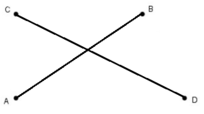
b) Đoạn thẳng AB cắt đoạn thẳng CD tại điểm
Cho hai đoạn thẳng MN và PQ cắt nhau tại điểm A. Hãy viết tên các cặp góc đối đỉnh
Viết tiếp vào chỗ chấm cho thích hợp :

a) Trung điểm của đoạn thẳng MN là điểm ... ứng với vạch số ...
b) S vừa là trung điểm của đoạn thẳng ... vừa là trung điểm của đoạn thẳng ...

a) Trung điểm của đoạn thẳng MN là điểm S ứng với vạch số 5000
b) S vừa là trung điểm của đoạn thẳng PQ, vừa là trung điểm của đoạn thẳng MN.
điền vào chỗ chấm:tam giác MNP là hình gồm 3 đoạn thẳng MN, NP,PQ khi 3 điểm M,N,P.................
tam giác MNP là hình gồm 3 đoạn thẳng MN, NP,PQ khi 3 điểm M,N,P thẳng hàng
điền vào chỗ chấm:tam giác MNP là hình gồm 3 đoạn thẳng MN, NP,PQ khi 3 điểm M,N,P.....ko thẳng hàng............
Vẽ hình theo diễn đạt:
a) K là giao điểm của 2 đoạn thẳng MN và PQ
b) Tia Cx cắt đoạn thẳng DE tại điểm N
c) Đường thẳng xy cắt đoạn thẳng ST tại điểm N
d) Đường thẳng a đi qua mút của đoạn thẳng HK
Cho tam giác ABC và một điểm I thuộc miền trong tam giác. Giả sử đường tròn ngoại tiếp tam giác IBC cắt các đoạn thẳng AB và AC lần lượt tại các điểm D và E. Gọi F là giao điểm của hai đường thẳng BE và CD. Đường thẳng ID và đường thẳng IE theo thứ tự cắt đường thẳng AF tại M và N.
1. Chứng minh rằng: đường tròn (C₁) ngoại tiếp tam giác BMN và đường tròn (C₂) ngoại tiếp tam giác CMN có độ dài bằng nhau.
2. Đường tròn (C₁) cắt đường thẳng AB và đường thẳng BE lần lượt tại P và T (P và T khác B). Đường tròn (C₂) cắt đường thẳng AC và đường thẳng CD lần lượt tại S và Q (S và Q khác C). Chứng minh rằng: ba đoạn thẳng MN, PQ và ST đồng qui tại trung điểm của mỗi đoạn.
Vẽ hình theo diễn đạt sau:
a)Hai đg thẳng m và n cắt nhau tại A,đg thẳng p cắt m tại B và cắt n tại C
b)Đg thẳng MN và đg thẳng PQ cắt nhau tại O
c)Lấy 3 điểm P,Q,S ko thẳng hàng.Vẽ 2 tia PQ,PS sau đó vẽ tia Px cắt đoạn thẳng QS tại điễm K nằm giữa 2 điểm Q và S
Cho tam giác MNP. Tại đỉnh M dựng góc xMN so le trong với góc N. Trên tia Mx lấy điểm Q sao cho đoạn thẳng MQ=NP, đoạn thẳng PQ cắt đoạn thẳng MN tại O.
a) chứng minh O là trung điểm đoạn thẳng MN.
b) chứng minh 2 tam giác MOP và NOQ bằng nhau.