Tiệm cận ngang và tiệm cận đứng của đồ thị hàm số y = x + 2 x - 1 là:
A.y=2;x=1
B.y=1;x=1
C.y=-2;x=1
D.y=1;x=-2
Xét các mệnh đề sau
(1). Đồ thị hàm số y = 1 2 x - 3 có hai đường tiệm cận đứng và một đường tiệm cận ngang
(2). Đồ thị hàm số y = x + x 2 + x + 1 x có hai đường tiệm cận ngang và một đường tiệm cận đứng
(3). Đồ thị hàm số y = x - 2 x - 1 x 2 - 1 có một đường tiệm cận ngang và hai đường tiệm cận đứng.
Số mệnh đề đúng là:
A. 0
B. 3
C. 2
D. 1
Đáp án D
Đồ thị hàm số y = 1 2 x - 3 có hai đường tiệm cận đứng và một đường tiệm cận ngang
Đồ thị hàm số y = x + x 2 + x + 1 x có 1 tiệm cận đứng là x = 0
Mặt khác lim x → + ∞ y = x + x 2 + x + 1 x = lim x → + ∞ x + x + 1 x + 1 x 2 x = 0 nên đồ thị hàm số có 2 tiệm cận ngang
Xét hàm số y = x - 2 x - 1 x 2 - 1 = x - 2 x - 1 x + 2 x - 1 x 2 - 1 = x - 1 x + 2 x - 1 x - 1 x > 1 2 suy ra đồ thị không có tiệm cận đứng. Do đó có 1 mệnh đề đúng
Hình vẽ bên là đồ thị của hàm số y=f(x). Tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y=f(x) là
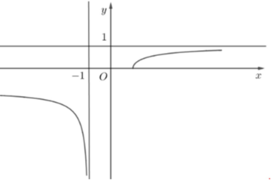
A. x=-1; y=1
B. x=1; y=-1
C. x=-1; y=-1
D. x=1; y=1
Quan sát đồ thị có ![]()
![]() là tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho.
là tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho.
Chọn đáp án A.
Đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y = 1 − 2 x − x + 2 là:
A. x = − 2 ; y = − 2
B. x = 2 ; y = − 2
C. x = − 2 ; y = 2
D. x = 2 ; y = 2
Đáp án là D.
Đồ thị có tiệm cận đứng và tiệm cận ngang lần lượt là: x = 2 ; y = 2.
Tìm số tiệm cận (bao gồm tiệm cận đứng và tiệm cận ngang) của đồ thị hàm số y = 4 x 2 + 5 2 x + 1 - x - 1
A. 3.
B. 1.
C. 2.
D. 4.
Chọn C.
Hàm số có tập xác định là 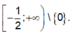
Ta có
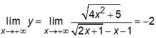
=> y = -2 là đường tiệm cận ngang của đồ thị hàm số đã cho.
Mặt khác,
![]()
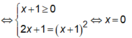
Với mọi x > 0 ta có ![]()
![]()
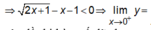
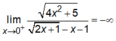
=> x = 0 là đường tiệm cận đứng của đồ thị hàm số đã cho.
Vậy hàm số đã cho có 2 đường tiệm cận.
Tìm số tiệm cận (bao gồm tiệm cận đứng và tiệm cận ngang) của đồ thị hàm số y = 4 x 2 + 5 2 x + 1 - x - 1
A. 3.
B. 1.
C. 2.
D. 4.
Tiệm cận ngang và tiệm cận đứng của đồ thị hàm số y = x + 2 x - 1 là:
A. y = 2, x = 1.
B. y = 1, x = 1.
C. y = -2, x = 1.
D. y = 1, x = -2.
Chọn B.
Ta có 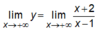
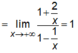
suy ra đường thẳng y = 1 là tiệm cận ngang của đồ thị hàm số.
Do ![]()
![]()
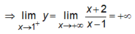
nên đường thẳng x = 1 là tiệm cận đứng của đồ thị hàm số.
Tìm số phát biểu đúng trong các phát biểu sau:
(1) Đồ thị hàm số y= x α với α > 0 nhận trục Ox làm tiệm cận ngang và nhận trục là tiệm cận đứng.
(2) Đồ thị hàm số y= x α với α > 0 không có tiệm cận.
(3) Đồ thị hàm số y = log a x với 1 < a ≠ 1 nhận trục Oy làm tiệm cận đứng và không có tiệm cận ngang.
(4) Đồ thị hàm số y=ax với 1 < a ≠ 1 nhận trục Ox làm tiệm cận ngang và không có tiệm cận đứng.
A. 2.
B. 1
C. 4
D. 3.
Phương pháp:
Dựa vào các tính chất của đồ thị hàm số mũ và hàm số logarit.
Cách giải:
Cả 4 phát biểu đều đúng
Chọn C
Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y = \(\dfrac{x+\sqrt{x^2+1}}{x+1}\)
Lời giải:
TXĐ: \((-\infty; -1)\cup (-1;+\infty)\)
\(\lim\limits_{x\to +\infty}y=\lim\limits_{x\to +\infty}\frac{1+\sqrt{1+\frac{1}{x}}}{1+\frac{1}{x}}=\frac{1+1}{1}=2\)
\(\lim\limits_{x\to -\infty}y=\lim\limits_{x\to -\infty}\frac{-1+\sqrt{1+\frac{1}{x^2}}}{-1+\frac{1}{-x}}=\frac{-1+1}{-1}=0\)
Do đó ĐTHS có 2 TCN là $y=0$ và $y=2$
\(\lim\limits_{x\to -1-}y=\lim\limits_{x\to -1-}\frac{x+\sqrt{x^2+1}}{x+1}=-\infty\) do \(\lim\limits_{x\to -1-}(x+\sqrt{x^2+1})=\sqrt{2}-1>0\) và \(\lim\limits_{x\to -1-}\frac{1}{x+1}=-\infty\)
Tương tự \(\lim\limits_{x\to -1+}y=+\infty\) nên $x=-1$ là TCĐ của đths
Vậy có tổng 3 TCN và TCĐ
Các đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm số y = 1 - x + x 3 3 + x là:
A. x=-3; y=1
B. x=-3; y=-1/2
C. x=3; y=1/2
D. x=3; y=-1/2