Cho hàm số y = f (x) thoả mãn f ( x ) + 2 f ( 1 - x ) = ( 2 x + 1 ) e x , ∀ x ∈ R Tích phân ∫ 0 1 3 f ( 3 x ) d x bằng
A. e + 1 3
B. e + 1
C. e + 1 9
D. 3 e + 1
PB
Những câu hỏi liên quan
Cho hàm số y=f(x) thoả mãn f(x)+xf(x/2x-1)=2 mọi x\{1;1/2}. Tính f(5)
a.Tìm các cặp số x,y thoả mãn\(|x^4-1|+|y^2-3|=0\)
b.Cho hàm số f(x) thoả mãn f(f(x))=x+10, biết f(2001)=2011
a, \(\left|x^4-1\right|\)\(+\left|y^2-3\right|=0\)
-Vì: $\left\{\begin{matrix}
|x^4-1|\geq 0 & \\
|y^2-3|\geq 0 &
\end{matrix}\right.$
-Để: $|x^4-1|+|y^2-3|=0$
-Thì:
$\Rightarrow \left\{\begin{matrix}
|x^4-1|=0 & \\
|y^2-3|=0 &
\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix}
x^4-1=0 & \\
y^2-3=0 &
\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix}
x^4=1 & \\
y^2=3 &
\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix}
x=\pm 1 & \\
y=\pm \sqrt{3} &
\end{matrix}\right.$
b, Đề thiếu kìa bạn!!
Đúng 0
Bình luận (0)
H24
SGK Kết nối tri thức và cuộc sống
17 tháng 8 2023 lúc 21:19
Cho hàm số \(f(x)\) thoả mãn \(f(1) = 2\) và \(f'(x) = {x^2}f(x)\) với mọi \(x\). Tính \(f''(1)\).
Cho hàm số f(x) xác định và liên tục trên R và có đạo hàm f'(x) thoả mãn f'(x) = (1 - x)(x+2)g(x) + 2023 với g(x) < 0, ∀x∈R. Hàm số y = f(1-x) + 2023x + 2024 nghịch biến trên khoảng nào?
Xác định một hàm số y f(x) thoả mãn đồng thời các điều kiện sauf(x) xác định trên R {1}
lim
x
→
1
f
(
x
)
+
∞
;
lim
x
→
+
∞
f...
Đọc tiếp
Xác định một hàm số y = f(x) thoả mãn đồng thời các điều kiện sau
f(x) xác định trên R\ {1}
lim x → 1 f ( x ) = + ∞ ; lim x → + ∞ f ( x ) = 2 ; lim x → - ∞ f ( x ) = 2
Chẳng hạn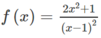 
.
Dễ dàng kiểm tra được rằng f(x) thoả mãn các điều kiện đã nêu
Đúng 0
Bình luận (0)
23. Cho hs y= f(x) có đạo hàm f'(x) =-x^2-1 . Với các số thực dương a,b thoả mãn a
Cho hàm số y = f(x) = 5^x. Số nguyên x thoả mãn f(x+1) - f(x) = 100 là
ta có f(x+1)-f(x)=100
=5^x+1-5^x=100
\(\Rightarrow\)x=2
Đúng 0
Bình luận (0)
Ta có f(x+1)- f(x) = 100 suy ra 5^x + 1-5^x =100 => x=2. HẾT
Đúng 0
Bình luận (0)
\(5^{x+1}-5^x=100\Leftrightarrow5^x.4=100\Leftrightarrow5^x=25\Leftrightarrow x=2\)
Đúng 0
Bình luận (0)
Cho hàm số yf(x) thoả mãn f(-2)3, f(2)2 và bảng xét dấu của đạo hàm như sau:Bất phương trình
3
f
(
x
)
+
m
≤
4
f
(
x
)
+
1
+
4
m
nghiệm đúng với mọi số thực
x
∈
-
2
;
2...
Đọc tiếp
Cho hàm số y=f(x) thoả mãn f(-2)=3, f(2)=2 và bảng xét dấu của đạo hàm như sau:
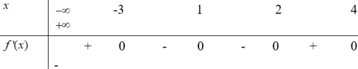
Bất phương trình 3 f ( x ) + m ≤ 4 f ( x ) + 1 + 4 m nghiệm đúng với mọi số thực x ∈ - 2 ; 2 khi và chỉ khi
A. m ∈ - 2 ; - 1
B. m ∈ - 2 ; - 1
C. m ∈ - 2 ; 3
D. m ∈ - 2 ; 3
Có 
Đặt t=f(x)+m bất phương trình trở thành: 
Vậy 
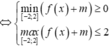
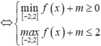
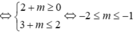
Chọn đáp án B.
Đúng 0
Bình luận (0)
Cho hàm số f(x) liên tục trên R+ và thoả mãn
∫
f
(
x
+
1
)
x
+
1
d
x
2
(
x
+
1
+
3...
Đọc tiếp
Cho hàm số f(x) liên tục trên R+ và thoả mãn ∫ f ( x + 1 ) x + 1 d x = 2 ( x + 1 + 3 ) x + 5 + C . Nguyên hàm của hàm số f(2x) trên tập R+ là
Cho hàm số
y
f
(
x
)
liên tục trên R và có hàm số
y
f
(
x
)
thoả mãn. Số cực trị của hàm số
y
f
(
x
)
là A. 3 B. 1 C. 0 D. 2
Đọc tiếp
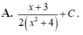
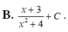
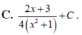
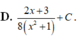
Cho hàm số y = f ( x ) liên tục trên R và có hàm số y = f ' ( x ) thoả mãn. Số cực trị của hàm số y = f ( x ) là
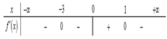
A. 3
B. 1
C. 0
D. 2
