Tổng số giá trị nguyên của m để phương trình x 3 + x ( x + 1 ) = m ( x 2 + 1 ) 2 có nghiệm thực là
A. 5
B. 4
C. 7
D. 0
Cho hàm số f x = x − 3 3 x 2 + 8. Tính tổng các giá trị nguyên của m để phương trình f x − 1 + m = 2 có đúng 3 nghiệm phân biệt.
A. -2
B. -6
C. 8
D. 4
Chọn B.
Phương pháp:

Bảng biến thiên:
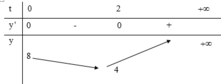
Phương trình đã cho có 3 nghiệm ⇔ phương trình ẩn t có hai nghiệm phân biệt trong đó có một nghiệm bằng 0 và một nghiệm dương ⇔ đường thẳng y = 2-m cắt đồ thị hàm số tại một điểm có hoành độ bằng 0 và điểm còn lại có hoành độ dương.

Cho S là tập hợp các giá trị thực của tham số m để phương trình 2 − x + 1 − x = m + x − x 2 có hai nghiệm phân biệt. Tổng các số nguyên trong S bằng
A. 11
B. 0
C. 5
D. 6
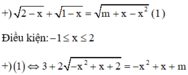
Đặt − x 2 + x = t ;
f x = − x 2 + x ; f ' x = − 2 x + 1
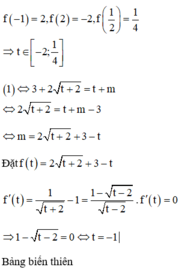

Chọn A
Cho S là tập hợp các giá trị thực của tham số m để phương trình 2 - x + 1 - x = m + x - x 2 có hai nghiệm phân biệt. Tổng các số nguyên trong S bằng
A. 11.
B. 0.
C. 5.
D. 6.
Đáp án A
+)![]() (
(![]() )
)
Điều kiện:![]()
+)![]()
Đặt:![]()
![]()
![]()
![]()
![]()
Đặt![]()
![]() .
.![]()
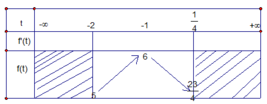
Bảng biến thiên
+) ![]()
Để phương trình có hai nghiệm phân biệt![]()
Do đó để phương trình có hai nghiệm phân biệt thì phương trình![]() có nghiệm
có nghiệm![]()
Từ bảng biến thiên![]() .
.
Cho hàm số y=f(x) có đồ thị như hình vẽ.
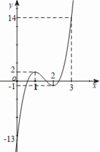
Tổng các giá trị nguyên m để phương trình
f(f(x) +1) = m có 3 nghiệm phân biệt bằng
A. 15
B. 1
C. 13
D. 11
Số giá trị nguyên của tham số m ∈ - 10 ; 10 để bất phương trình 3 + x + 6 - x - 18 + 3 x - x 2 ≤ m 2 - m + 1 nghiệm đúng ∀ x ∈ - 3 ; 6 là
A. 28
B. 20
C. 4
D. 19
Số giá trị nguyên của tham số m ∈ - 10 ; 10 để bất phương trình 3 + x + 6 - x - 18 + 3 x - x 2 ≤ m 2 -m+1 nghiệm đúng ∀ x ∈ - 3 ; 6 là
A. 28
B. 20
C. 4
D. 19
Cho phương trình
\(\left(m-1\right)x^2-2\left(m-3\right)x+m+1\)1=0
Với điều kiện của m để phương trình có 2 nghiệm x1, x2, gọi S và P lần lượt là tổng và tích của 2 nghiệm của phương trình. Tìm các giá trị của m để S và P là các số nguyên
Cho phương trình (2m−5)x2 −2(m−1)x+3=0 (1); với m là tham số thực
1) Tìm m để phương trình (1) có một nghiệm bằng 2, tìm nghiệm còn lại.
3) Tìm giá trị của m để phương trình đã cho có nghiệm
4) Xác định các giá trị nguyên của để phương trình đã cho có hai nghiệm phân biệt đều nguyên dương
1) điều kiện của m: m khác 5/2
thế x=2 vào pt1 ta đc:
(2m-5)*4 - 4(m-1)+3=0 <=> 8m-20-4m+4+3=0<=> 4m = 13 <=> m=13/4 (nhận)
lập △'=[-(m-1)]2-*(2m-5)*3 = (m-4)2
vì (m-4)2 ≥ 0 nên phương trình có nghiệm kép => x1= x2 =2
3) vì △'≥0 với mọi m nên phương trình đã cho có nghiệm với mọi m
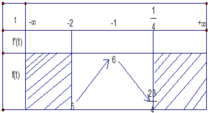
Tìm tổng tất cả các giá trị nguyên của m để phương trình 4 1 + x + 4 1 - x = ( m + 1 ) ( 2 2 + x - 2 2 - x ) + 16 - 8 m có nghiệm trên 0 ; 1
A. 2.
B. 5.
C. 4.
D. 3.
Đáp án D.
Phương trình tương đương với

Đặt 2 x - 1 2 x = t → 4 x + 1 4 x = t 2 + 2 . Xét hàm số t ( x ) = 2 x - 1 2 x trên 0 ; 1 .
Đạo hàm t ' ( x ) = 2 x . ln 2 + ln 2 2 x > 0 , ∀ x ∈ 0 ; 1 ⇒ Hàm số t ( x ) luôn đồng biến trên 0 ; 1 . Suy ra min x ∈ 0 ; 1 t ( x ) = t ( 0 ) = 0 và max x ∈ 0 ; 1 t ( x ) = t ( 1 ) = 3 2 . Như vậy t ∈ 0 ; 3 2 .
Phương trình (1) có dạng:
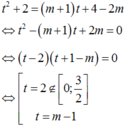
Phương trình (1) có nghiệm t ∈ 0 ; 1 ⇔ phương trình ẩn t có nghiệm t ∈ 0 ; 3 2 ⇔ 0 ≤ m - 1 ≤ 3 2 ⇔ 1 ≤ m ≤ 5 2 . Mà m ∈ ℤ nên m ∈ 1 ; 2 . Tổng tất cả các giá trị nguyên của m bằng 3.