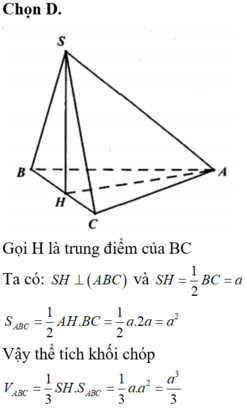
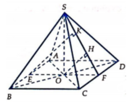
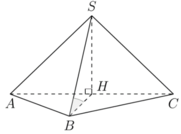
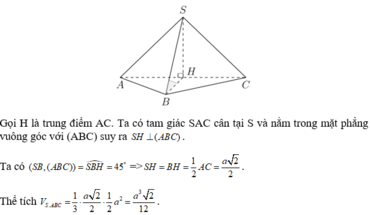
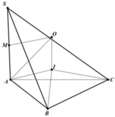
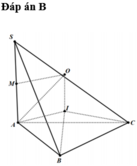
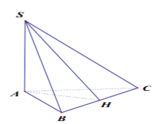
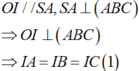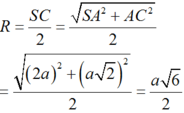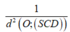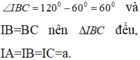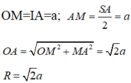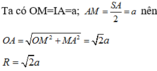Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, AB=2a, S A B ^ = S C B ^ = 90 0 và góc giữa đường thẳng AB và mặt phẳng (SBC) bằng 30 0 . Tính thể tích V của khối chóp đã cho.
A. V = a 3 3 3
B. V = 4 a 3 3 9
C. V = 2 a 3 3 3
D. V = 8 a 3 3 3