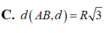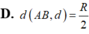Cho hai hình trụ có bán kính đường tròn đáy lần lượt là R 1 ; R 2 và chiều cao lần lượt là h 1 ; h 2 . Nếu hai hình trụ có cùng thể tích và h 1 h 2 = 9 4 thì tỉ số R 1 R 2 bằng
A. 3 2
B. 2 3
C. 9 4
D. 4 9
PB
Những câu hỏi liên quan
Cho hình trụ có chiều cao
h
a
3
bán kính
r
a
. Gọi O và O’ lần lượt là tâm của hai hình tròn đáy. Hai điểm A,B thuộc hai đường tròn đáy sao cho
A
B
2
a
. Tính số đo góc giữa hai đường thẳng AB và OO’ A.
A
B
,
O
O...
Đọc tiếp
Cho hình trụ có chiều cao h = a 3 bán kính r = a . Gọi O và O’ lần lượt là tâm của hai hình tròn đáy. Hai điểm A,B thuộc hai đường tròn đáy sao cho A B = 2 a . Tính số đo góc giữa hai đường thẳng AB và OO’
A. A B , O O ' = 30 0
B. A B , O O ' = 60 0
C. A B , O O ' = 45 0
D. A B , O O ' = 90 0
Một hình trụ có bán kính r và chiều cao h = r √3
Cho hai điểm A và B lần lượt nằm trên hai đường tròn đáy sao cho góc giữa đường thẳng AB và trục của hình trụ bằng 30 o .Tính khoảng cách giữa đường thẳng AB và trục của hình trụ.
Cho một hình trụ có bán kính đáy bằng R và có chiều cao bằng
R
3
Hai điểm A,B lần lượt nằm trên hai đường tròn đáy sao cho góc giữa AB và trục của hình trụ bằng
30
°
. Khoảng cách giữa AB và trục của hình trụ bằng:
Đọc tiếp
Cho một hình trụ có bán kính đáy bằng R và có chiều cao bằng R 3 Hai điểm A,B lần lượt nằm trên hai đường tròn đáy sao cho góc giữa AB và trục của hình trụ bằng 30 ° . Khoảng cách giữa AB và trục của hình trụ bằng:
Cho hình trụ có bán kính đáy r, gọi O và O là tâm của hai đường tròn đáy với OO2r. Một mặt cầu tiếp xúc với hai đáy của hình trụ tại O và O. Gọi
V
C
và
V
T
lần lượt là thể tích của khối cầu và khối trụ. Khi đó
V
C
V
T
bằng
Đọc tiếp
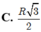
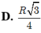
Cho hình trụ có bán kính đáy r, gọi O và O' là tâm của hai đường tròn đáy với OO'=2r. Một mặt cầu tiếp xúc với hai đáy của hình trụ tại O và O'. Gọi V C và V T lần lượt là thể tích của khối cầu và khối trụ. Khi đó V C V T bằng
Cho hình trụ có chiều cao
h
a
3
, bán kính đáy
r
a
. Gọi O, O lần lượt là tâm của hai đường tròn đáy. Trên hai đường tròn đáy lần lượt lấy hai điểm A, B sao cho hai đường thẳng AB và OO chéo nhau và góc giữa hai đường thẳng AB và OO bằng
30
°
. Khoảng cách giữa hai đường thẳng AB và OO bằng: A.
a
6...
Đọc tiếp
Cho hình trụ có chiều cao h = a 3 , bán kính đáy r = a . Gọi O, O' lần lượt là tâm của hai đường tròn đáy. Trên hai đường tròn đáy lần lượt lấy hai điểm A, B sao cho hai đường thẳng AB và OO' chéo nhau và góc giữa hai đường thẳng AB và OO' bằng 30 ° . Khoảng cách giữa hai đường thẳng AB và OO' bằng:
A. a 6 2 .
B. a 3 .
C. a 3 2
D. a 6 .
Cho hình trụ có chiều cao h a
3
, bán kính đáy r a. Gọi O,O’ lần lượt là tâm của hai đường tròn đáy. Trên hai đường tròn đáy lần lượt lấy hai điểm A, B sao cho hai dường thẳng AB và OO’ chéo nhau và góc giữa hai đường thẳng AB với OO’ bằng 300. Khoảng cách giữa hai đường thẳng AB và OO’ bằng : A.
a
6
B.
a
6...
Đọc tiếp
Cho hình trụ có chiều cao h = a 3 , bán kính đáy r = a. Gọi O,O’ lần lượt là tâm của hai đường tròn đáy. Trên hai đường tròn đáy lần lượt lấy hai điểm A, B sao cho hai dường thẳng AB và OO’ chéo nhau và góc giữa hai đường thẳng AB với OO’ bằng 300. Khoảng cách giữa hai đường thẳng AB và OO’ bằng :
A. a 6
B. a 6 2
C. a 3
D. a 3 2
Đáp án D.
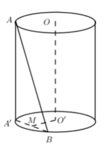
Phương pháp :
+) Xác định mặt phẳng (P) chứa AB và song song với OO’.
+) d(OO’;AB) = D(OO’;(P))
Cách giải :
Dựng AA’//OO’ ta có: (OO’;AB) = (AA’;AB) = A’AB = 300
Gọi M là trung điểm của A’B ta có:
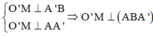
=>d(OO’;AB) = d(OO’;(ABA’)) = d(O’;(ABA’)) = O’M
Xét tam giác vuông ABA’ có 
Xét tam giác vuông O’MB có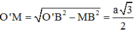 
Đúng 0
Bình luận (0)
Cho hình trụ có chiều cao ha
3
bán kính đáy ra. Gọi O,O’ lần lượt là tâm của hai đường tròn đáy. Trên hai đường tròn đáy lần lượt lấy hai điểm A, B sao cho hai dường thẳng AB và OO’ chéo nhau và góc giữa hai đường thẳng AB với OO’ bằng
30
0
. Khoảng cách giữa hai đường thẳng AB và OO’ bằng :
Đọc tiếp
Cho hình trụ có chiều cao h=a 3 bán kính đáy r=a. Gọi O,O’ lần lượt là tâm của hai đường tròn đáy. Trên hai đường tròn đáy lần lượt lấy hai điểm A, B sao cho hai dường thẳng AB và OO’ chéo nhau và góc giữa hai đường thẳng AB với OO’ bằng 30 0 . Khoảng cách giữa hai đường thẳng AB và OO’ bằng :
Cho hình trụ có bán kính R và chiều cao
3
R
. Hai điểm A, B lần lượt nằm trên hai đường tròn đáy sao cho góc giữa AB và trục d của hình trụ bằng
30
°
. Tính khoảng cách giữa AB và trục của hình trụ. A.
d
A
B
,
d
R
3
2
B.
d...
Đọc tiếp
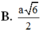
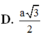
Cho hình trụ có bán kính R và chiều cao 3 R . Hai điểm A, B lần lượt nằm trên hai đường tròn đáy sao cho góc giữa AB và trục d của hình trụ bằng 30 ° . Tính khoảng cách giữa AB và trục của hình trụ.
A. d A B , d = R 3 2
B. d A B , d = R
C. d A B , d = R 3
D. d A B , d = R 2
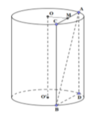
Gọi O,
O
'
lần lượt là tâm của hai hình tròn đáy (như hình vẽ). Dựng AD, BC song song O
O
'
, với
C
∈
O
;
D
∈
O
'
. Gọi M là trung điểm của AC.
Ta có:
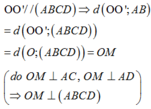
Ta có:
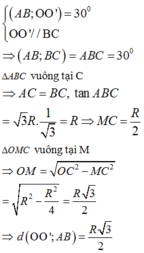
Chọn: A
Đúng 0
Bình luận (0)
Cho hình trụ có bán kính R và chiều cao
3
R
. Hai điểm A, B lần lượt nằm trên hai đường tròn đáy sao cho góc giữa AB và trục d của hình trụ bằng
30
°
. Tính khoảng cách giữa AB và trục của hình trụ
Đọc tiếp
Cho hình trụ có bán kính R và chiều cao 3 R . Hai điểm A, B lần lượt nằm trên hai đường tròn đáy sao cho góc giữa AB và trục d của hình trụ bằng 30 ° . Tính khoảng cách giữa AB và trục của hình trụ
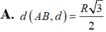
