Cho hàm số y = f x có đồ thị (C) như hình vẽ. Tính A = f ' 1 − f ' 2 − f ' 3
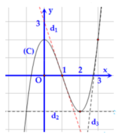
A. A = 6
B. A = -6
C. A = 0
D. A = -12
Cho hàm số y=f( x) = ax3+ bx2+ cx+ d có đồ thị (C). Biết rằng đồ thị (C) đi qua gốc toạ độ và đồ thị hàm số y=f’( x) cho bởi hình vẽ bên. Tính f( 3) –f( 1) ?
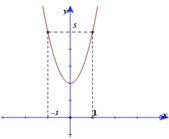
A. 24.
B. 28.
C. 26.
D. 21.
Ta có đạo hàm : f’ (x) = 3ax2+ 2bx+ c.
Dựa vào đồ thị hàm số y= f’(x) ; ta thấy đồ thị hàm số y= f’(x) là parabol có trục đối xứng là trục tung nên b= 0
+ Đồ thị hàm số y= f’(x) đi qua 2 điểm (1; 5) và (0; 2) ta tìm được: a=1 và c=2.
Suy ra: f’(x) = 3x2+ 2 và f( x) = x3+ 2x+ d,
+ Do đồ thị hàm số (C) đi qua gốc toạ độ nên 0=0+0+ d
Suy ra: d= 0.
Khi đó ta có: f(x) =x3+ 2x và f( 3) –f(2) =21
Chọn D.
Cho hàm số y = f ( x ; m ) có đồ thị hàm số y = f ' ( x ; m ) như hình vẽ
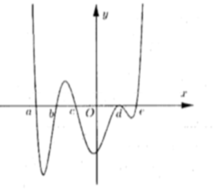
Biết f ( a ) > f ( c ) > 0 ; f ( b ) < 0 < f ( e ) Hỏi hàm số y = f ( x , m ) có bao nhiêu điểm cực trị?
A. 5
B. 7
C. 9
D. 10
Cho hàm số y = f x = ax 3 + bx 2 + cx + d có đồ thị (C), đồ thị y = f '(x) như hình vẽ bên. Biết đồ thị hàm số y = f(x) có điểm cực tiểu có tung độ bằng 2 3 . Tính 3 a − b + 5 c + 3 d bằng?
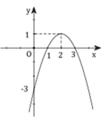
A. -16
B. -12
C. 9
D. 10
Đáp án B
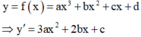
Nhìn vào đồ thị của hàm số y = f '(x) ta nhận thấy đồ thị hàm số đi qua các điểm (1;0), (3;0), (2;1) nên có hệ phương trình sau:
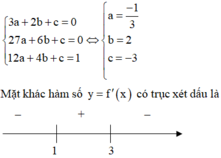
Nên đồ thị hàm số y = f(x) có điểm cực tiểu có tung độ bằng 2 3
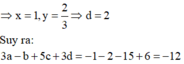
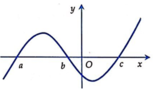
Cho hàm số y=f(x) có đồ thị y=f’(x) như hình vẽ bên. Biết f(a)>0, hỏi đồ thị hàm số y=f(x) cắt trục hoành tại nhiều nhất bao nhiêu điểm?
A. 1 điểm
B. 2 điểm
C. 3 điểm
D. 4 điểm
Cho hàm số y = f(x) có đồ thị y = f''(x) như hình vẽ bên. Biết f (a) > 0, hỏi đồ thị hàm số y = f (x) cắt trục hoành tại nhiều nhất bao nhiêu điểm?
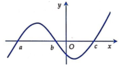
A. 1 điểm
B. 2 điểm
C. 3 điểm
D. 4 điểm
Đáp án B.
Từ đồ thị hàm số y = f ' ( x ) ta có bảng biến thiên:

Từ bảng biến thiên ta có f ( b ) > f ( a ) > 0
Quan sát đồ thị y = f ' ( x ) , dùng phương pháp tích phân để tính diện tích.
Ta có ∫ a b f ' ( x ) d x < ∫ a c 0 - f ' ( x ) d x ⇒ f ( c ) < f a
Nếu f c < 0 thì đồ thị hàm số y = f ( x ) cắt trục hoành tại 2 điểm phân biệt.
Nếu f c = 0 thì đồ thị hàm số y = f ( x ) tiếp xúc với trục hoành tại 1 điểm.
Nếu f c > 0 thì đồ thị hàm số y = f ( x ) không cắt trục hoành.
Vậy đồ thị hàm số y = f ( x ) cắt trục hoành tại nhiều nhất 2 điểm.
Cho hàm số y = f(x). Hàm số y = f’(x) có
đồ thị như hình vẽ. Hàm số y = f(lnx +1) nghịch biến
trên khoảng
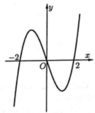
A. (e;+∞).
B. (1/e;e).
C. 1 e 3 ; 1 e
D.(0;e)
Cho hàm số y=f(x) Hàm số y=f’(x) có đồ thị như hình vẽ. Hàm số y=f(-lnx+1) nghịch biến trên khoảng
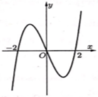
A. (e;+∞)
B. (1/e;e)
C. 1 e 3 ; e
D. (0;e)
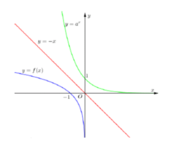
Biết hai hàm số y = a x , y = f ( x ) có đồ thị như hình vẽ đồng thời đồ thị của hai hàm số này đối xứng nhau qua đường thẳng y = - x . Tính f - a + f - a 2
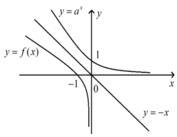
A. -3
B. 4
C. 5
D. đáp án khác
Biết hai hàm số y = a x ; y = f ( x ) có đồ thị như hình vẽ đồng thời đồ thị của hai hàm số này đối xứng nhau qua đường thẳng y = -x. Tính f ( - a ) + f ( - a 2 )
A. -3
B. 4
C. 5
D. 3